1. (2022·李沧模拟) 问题提出

我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，而解决问题的策略一般要进行一定的转化，其中“作差法”就是常用的方法之一．所谓“作差法”：就是通过作差、变形，并利用差的符号确定他们的大小． 例如：

对于任意两个代数式M，N的大小比较，有下面的方法：

当M－N＞0时，M ＞N；

当M－N＝0时，M＝N；

当M－N＜0时，M ＜N.

反过来也成立. 因此，我们把这种比较两个代数式大小的方法叫做“作差法”．

对于比较两个正数a，b的大小，我们还可以用它们的平方进行比较：

∵a²－b²＝（a＋b）（a－b），a＋b＞0，

∴（a²－b²）与（a－b）的符号相同.

当a²－b²＞0时，a－b＞0，得a＞b；

当a²－b²＝0时，a－b＝0，得a＝b；

当a²－b²＜0时，a－b＜0，得a＜b．

问题解决

1. （1） 课堂上，老师让同学们制作几种几何体，张丽同学用了3张A4纸，7张B5纸；李明同学用了2张A4纸，8张B5纸. 设每张A4纸的面积为x，每张B5纸的面积为y，且x＞y，张丽同学的用纸总面积为S₁ ， 李明同学的用纸总面积为S₂. 回答下列问题：

   ①S₁＝      ▲ （用含x，y的代数式表示）；

   S₂＝      ▲ （用含x，y的代数式表示）；

   ②试比较谁的用纸总面积更大？

3. （2） 如图1所示，要在燃气管道l上修建一个泵站，向A，B两镇供气，已知A，B到l的距离分别是3km，4km（即AC＝3km，BE＝4km），AB＝x km，现设计两种方案：

   

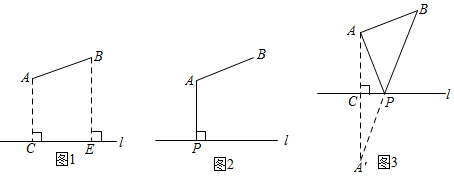
   方案一：如图2所示，AP⊥l于点P，泵站修建在点P处，该方案中管道长度a₁=AB+AP.

   方案二：如图3所示，点A′与点A关于l对称，A′B与l相交于点P，泵站修建在点P处，该方案中管道长度a₂＝AP+BP.

   ①在方案一中，a₁＝      ▲ km（用含x的代数式表示）；

   ②在方案二中，a₂＝      ▲ km（用含x的代数式表示）；

   ③请分析说明哪种方案铺设的输气管道较短？

5. （3） 甲、乙两位采购员同去一家饲料公司购买两次饲料，两次购买的价格有变化，两位采购员的购货方式也不同，其中，甲每次购买1000kg，乙每次用去1000元，而不管购买多少饲料. 设两次购买的饲料单价分别为m元/kg和n元/kg（m，n是正数，且m≠n），试分析哪位采购员的购货方式合算？