1. (2021七上·信都期中) 我国著名数学家华罗庚说过“数缺形时少直观，形少数时难人微”，数形结合是解决数学问题的重要思想方法．请阅读下列材料：

材料（一）：代数式|x﹣2|的几何意义是数轴上表示有理数x所对应的点与表示有理数2所对应的点之间的距离；因为|x＋1|＝|x﹣（﹣1）|，所以|x＋1|的几何意义就是数轴上表示有理数x所对应的点与表示有理数﹣1所对应的点之间的距离．

材料（二）：如图，点A、B、P分别表示有理数数﹣1、2、x，AB＝3，

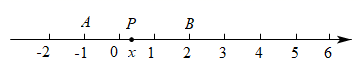
∵|x＋1|＋|x﹣2|的几何意义是线段PA与PB的长度之和，∴当点P在线段AB上时，PA＋PB＝3，当点P在点A的左侧或点B的右侧时，PA＋PB＞3，

∴|x＋1|＋|x﹣2|的最小值是3；

解决问题：

1. （1） 在数轴上，若点M表示的数为﹣2，点Q表示的数为1，点N表示的数为6，请画出一条数轴，标出点M、Q、N的位置，

   ①线段NQ＝            ▲       ；

   ②若数轴上点C表示的有理数为x，求|x＋2|＋|x﹣6|的最小值．

3. （2） 若代数式|x＋a|＋|x﹣3|的最小值是2，求a的值．