河北省邢台市信都区2021-2022学年七年级上学期期中数学...

更新时间：2022-06-30 浏览次数：108 类型：期中考试

一、单选题

1. (2021七上·信都期中) 下列各图中，表示“射线 $\text{[math]}$ ”的中（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021七上·信都期中) 有如下两个问题：①7和﹣7是一对相反数；②﹣7和﹣ $\text{[math]}$ 是一对倒数，则有（）

A . ①正确，②错误 B . ①、②均正确 C . ①错误，②正确 D . ①、②均错误

答案解析收藏纠错 + 选题
3. (2021七上·信都期中) 检测4袋茶叶的质量，超过标准的克数记为正数，不足的克数记为负数，从重量的角度来看，最接近标准的那一袋是（）

A . +3 B . -0.3 C . +0.2 D . -3.6

答案解析收藏纠错 + 选题
4. (2021七上·信都期中) 围成下列这些立体图形的各个面中，都是平的面为（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2021七上·信都期中) 如图，在应用有理数减法法则，进行运算时，下列说法正确的是（）

A . ①、②均需变成“＋” B . 只有①变成“＋” C . 只有①变成“×” D . 只有②变成“＋”

答案解析收藏纠错 + 选题
6. (2021七上·信都期中) 若6□（﹣3）＝﹣2，则□表示的运算符号是（）

A . ＋ B . ﹣ C . × D . ÷

答案解析收藏纠错 + 选题
7. (2021七上·信都期中) 如图，将甲，乙两把尺子拼在一起，两端重合，如果甲尺经校定是直的，那么乙尺不是直的，判断依据是（）

A . 两点之间直线最短 B . 经过一点有且只有一条直线 C . 经过两点有且只有一条直线 D . 线段可以向两个方向延长

答案解析收藏纠错 + 选题
8. (2021七上·信都期中) 在下列执行异号两数相加的步骤中，错误的是（）
①求两个有理数的绝对值；②比较两个有理数绝对值的大小；③将两个有理数绝对值的和作为结果的绝对值；④将绝对值较大数的符号作为结果的符号.

A . ① B . ② C . ③ D . ④

答案解析收藏纠错 + 选题
9. (2021七上·恩阳期中) 如图，在数轴上，注明了四段的范围，若某段上有两个整数，则这段是（）

A . 段① B . 段② C . 段③ D . 段④

答案解析收藏纠错 + 选题
10. (2022七上·卢龙期中) 若a表示正整数，且﹣ $\text{[math]}$ ＜﹣ $\text{[math]}$ ，则a的值可以是（）

A . 1 B . 3 C . 5 D . 7

答案解析收藏纠错 + 选题
11. (2021七上·信都期中) 若两个图形有公共点，则称这两个图形相交，否则称它们不相交．如图，直线PA、PB和线段AB将平面分成五个区域（不包含边界），若线段PQ与线段AB相交，则点Q落在的区域是（）

A . ① B . ② C . ③ D . ④或⑤

答案解析收藏纠错 + 选题
12. (2021七上·信都期中) 为计算简便，把（﹣2.4）﹣（﹣4.7）﹣（＋0.5）＋（﹣3.5）写成省略加号的和的形式，正确的是（）

A . ﹣2.4﹣4.7﹣0.5﹣3.5 B . ﹣2.4＋4.7＋0.5﹣3.5 C . ﹣2.4＋4.7﹣0.5﹣3.5 D . ﹣2.4＋4.7﹣0.5＋3.5

答案解析收藏纠错 + 选题
13. (2022七上·卢龙期中) 计算：72°22′+50°40′30″的结果是（　　）

A . 122°62′30″ B . 123°2′30″ C . 122°2′30″ D . 123°12′30″

答案解析收藏纠错 + 选题
14. (2021七上·信都期中) 嘉淇在用直尺和圆规作一个角等于已知角的步骤如下：
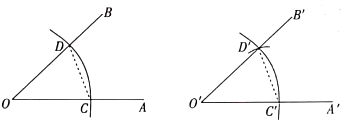
已知：∠AOB
求作：∠A′O′B′，使∠A′O′B′＝∠AOB
作法：⑴如图，以点O为圆心，m为半径画弧，分别交OA，OB于点C，D；
⑵画一条射线O′A′，以点O′为圆心，n为半径画弧，交O′A′于点C′；
⑶以点C′为圆心，p为半径画弧，与第（2）步中所画的弧相交于点D′；
⑷过点D′画射线O′B′，则∠A′O′B′＝∠AOB．
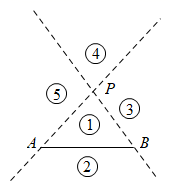
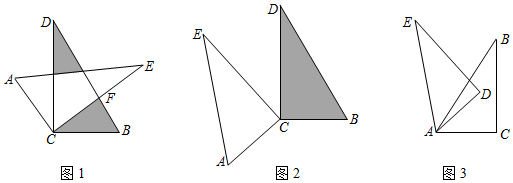
下列说法正确的是（）

A . m＝p＞0 B . n＝p＞0 C . p＝ $\text{[math]}$ n＞0 D . m＝n＞0

答案解析收藏纠错 + 选题

二、填空题

15. (2021七上·信都期中) 如图所示，用量角器度量∠AOB，可以读出∠AOB的度数为，∠AOB的余角的度数为．

答案解析收藏纠错 + 选题
16. (2023七上·城中月考) 在计算 $\text{[math]}$ 这一变形依据了，此题的计算结果是．

答案解析收藏纠错 + 选题
17. (2021七上·信都期中) 如图，线段AB上的点数与线段的总数有如下关系：如果线段AB上有三个点时，线段总共有 $\text{[math]}$ ＝3条，如果线段AB上有4个点时，线段总数有 $\text{[math]}$ ＝6条，如果线段AB上有5个点时，线段总数共有 $\text{[math]}$ ＝10条，……
1. （1）当线段AB上有6个点时，线段总数共有条；
2. （2）某学校七年级共有10个班进行辩论赛，规定进行单循环赛（每两班赛一场），那么该校七年级的辩论赛的场数是．
答案解析收藏纠错 + 选题

三、解答题

18. (2021七上·信都期中) 把下面一组数填入图中相应的位置，并填写公共部分的名称.0.7，﹣10，＋3.4，﹣4 $\text{[math]}$ ， 0，85，0.4

答案解析收藏纠错 + 选题
19. (2021七上·信都期中) 如图，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD中点．
1. （1）指出旋转中心．
2. （2）若∠BAE＝60°，求出旋转角的度数．
3. （3）若AB＝4，求AE的长．
答案解析收藏纠错 + 选题
20. (2021七上·信都期中) 老师设计了接力游戏，用合作的方式完成有理数运算，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：
1. （1）接力中，计算错误的学生是；
2. （2）请给出正确的计算过程．
答案解析收藏纠错 + 选题
21. (2021七上·信都期中) 如图，已知点A、B、C、D、E在同一直线上，且AC＝BD，E是线段BC的中点.
1. （1）点E是线段AD的中点吗？说明理由；
2. （2）当AD＝10，AB＝3时，求线段BE的长度.
答案解析收藏纠错 + 选题

22. (2021七上·单县期中) 某仓库在一周的货品运输中，进出情况如表（进库为正，出库为负，单位：吨）：

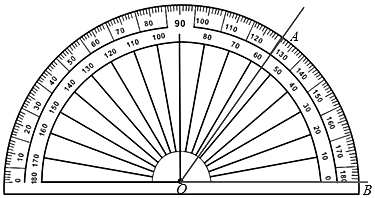
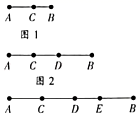
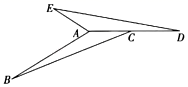
星期一	星期二	星期三	星期四	星期五	星期六	星期天	合计
＋26	﹣16	＋42	﹣30		﹣25	﹣9	＋6

表中星期五的进出数被墨水涂污了.

（1）请你算出星期五的进出数；
（2）如果进出的装卸费都是每吨10元，那么这一周要付多少元装卸费？

答案解析收藏纠错 + 选题

23. (2021七上·信都期中) 如图，小明将两块完全相同的直角三角形纸片的直角顶点C叠放在一起，若保持△BCD不动，将△ACE绕直角顶点C旋转．
1. （1）论证：如图1，如果CD平分∠ACE，说明CE平分∠BCD．
2. （2）发现：如图1，若∠DCE＝35°，则∠ACB＝°；若∠ACB＝140°，则∠DCE＝°；
3. （3）总结：当直角三角形ACE纸片绕直角顶点C旋转到如图1的位置时，猜想∠ACB与∠DCE的数量关系为 ▲ ；当△ACE绕直角顶点C旋转到如图2的位置时，上述关系是否依然成立，请说明理由；
4. （4）拓展：在图3中，将直角三角形ADE纸片绕顶点A逆时针旋转40°角到如图的位置，已知∠CAE＝100°，直接写出∠BAD的度数．
答案解析收藏纠错 + 选题
24. (2021七上·信都期中) 我国著名数学家华罗庚说过“数缺形时少直观，形少数时难人微”，数形结合是解决数学问题的重要思想方法．请阅读下列材料：
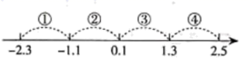
材料（一）：代数式|x﹣2|的几何意义是数轴上表示有理数x所对应的点与表示有理数2所对应的点之间的距离；因为|x＋1|＝|x﹣（﹣1）|，所以|x＋1|的几何意义就是数轴上表示有理数x所对应的点与表示有理数﹣1所对应的点之间的距离．
材料（二）：如图，点A、B、P分别表示有理数数﹣1、2、x，AB＝3，
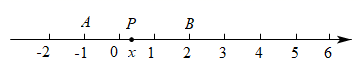
∵|x＋1|＋|x﹣2|的几何意义是线段PA与PB的长度之和，∴当点P在线段AB上时，PA＋PB＝3，当点P在点A的左侧或点B的右侧时，PA＋PB＞3，
∴|x＋1|＋|x﹣2|的最小值是3；
解决问题：
1. （1）在数轴上，若点M表示的数为﹣2，点Q表示的数为1，点N表示的数为6，请画出一条数轴，标出点M、Q、N的位置，
  ①线段NQ＝ ▲ ；
  ②若数轴上点C表示的有理数为x，求|x＋2|＋|x﹣6|的最小值．
2. （2）若代数式|x＋a|＋|x﹣3|的最小值是2，求a的值．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

河北省邢台市信都区2021-2022学年七年级上学期期中数学...

副标题：

*注意事项：

河北省邢台市信都区2021-2022学年七年级上学期期中数学...

试题分析

总体分析

题量分析

难度分析

知识点分析