1. (2022七下·金湖期末) 【原题重现】例：如图1，AC、BD相交于点O，求证：∠A＋∠B＝∠C＋∠D

 

1. （1）

   某数学兴趣小组同学对此题展开了探究讨论.

   【解法再探】课本利用“三角形内角和是180°”和“对顶角相等”对此题进行了证明，小明同学提出了另外一种证明方法，如下为思路框图：

   

   完成框图填空：①，②，③；

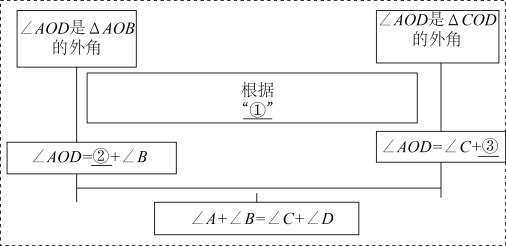
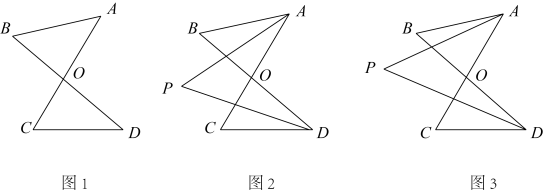
3. （2） 【变式拓展】小慧同学把图1中线段AC与BD相交所组成的结构称为“8字形”，她对原题进行了改编：如图2，AC、BD相交于点O ， AP、DP分别是∠BAC和∠BDC内的一条射线，它们相交于点P ， 请你根据（1）的结论写出关于∠P的两个关系式为：
   ①式∠P＋∠BDP＝，②式∠P＋∠CAP＝；
   小明进一步思考：若AP、DP分别是∠BAC和∠BDC的角平分线，由∠BAC＋∠B＝∠BDC＋∠C ， 得③式∠BAC－∠BDC＝∠C－∠B ， 由①式、③式（或②式、③式）联立、转化、整理可得∠P与∠B、∠C之间的关系，结论为：∠P＝；
5. （3） 【发现生成】小慧同学为了寻找规律，再次改变条件：如图3，AC、BD相交于点O ， ∠BAP=∠BAC，∠BDP=∠BDC，探索∠P与∠B、∠C之间的关系．请你写出解答过程；
7. （4） 若把（3）中的“”都改为“”，则∠P与∠B、∠C之间的关系为∠P＝.