1. (2022七下·太原期末) 阅读下面材料，完成相应的任务：

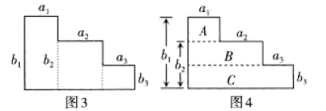
阿贝尔公式 数学界三大奖项之一的阿贝尔奖，是为了纪念挪威著名数学家阿贝尔所设．阿贝尔是近代数学发展的先驱，他年轻时利用阶梯图形，发现了重要的恒等式——阿贝尔公式． 如右图，用两种方法将一个二级阶梯图形分别分割成两个长方形．按图1的方法，该阶梯图形的面积为；按图2的方法，长方形①的面积为 ， 长方形②的面积为 ， 根据图1、图2面积相等，可得到二级阶梯图形对应的阿贝尔公式： ．

任务：

1. （1） 推理验证：材料中的阿贝尔公式可用代数运算验证，请补全如下说理过程：

   因为右边＝．

   左边＝a₁b₁＋a₂b₂ ， 左边＝右边，

   所以，a₁b₁＋a₂b₂＝a₁（b₁－b₂）＋（a₁＋a₂）b₂ ．

3. （2） 类比探究：如下图，用两种方法将一个三级阶梯图形分别分割成三个长方形．

   ①图4中长方形B的长为a₁＋a₂ ， 宽为  ▲  ；

   ②由图3、图4面积相等，可得三级阶梯图形对应的阿贝尔公式为：a₁b₁＋a₂b₂＋a₃b₃＝a_l（b_l－b₂）＋  ▲  ＋  ▲   ．

   请补全该公式，并进行验证．