1. (2022七上·义乌月考) 概念学习：

现规定：求若干个相同的有理数（均不等于0）的商的运算叫做除方，比如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等，类比有理数的乘方，我们把2÷2÷2写作2^③ ， 读作“2的圈3次方”，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）写作（﹣3）^④ ， 读作“（﹣3）的圈4次方”，一般地把（a≠0）写作a^ⓝ ， 读作“a的圈n次方”．

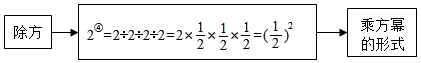
初步探究：

1. （1） 直接写出计算结果：3^②＝；（﹣）^③＝；
3. （2） 下列关于除方说法中，错误的有

   A．任何非零数的圈2次方都等于1

   B．任何非零数的圈3次方都等于它的倒数

   C．负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数

   D．圈n次方等于它本身的数是1或﹣1．
   深入思考： 我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，那么有理数的除方运算如何转化为乘方运算呢？

5. （3）
   比较：（﹣2）^⑩（﹣4）^⑩；（填“＞”“＜”或“＝”）
7. （4） 计算：﹣1^⑥+4²÷（﹣）^④×（﹣7）^③ ．