苏科版(2024)数学七上2.7 有理数的混合运算同步练习

更新时间：2024-08-20 浏览次数：15 类型：同步测试

一、选择题

1. (2024七上·鄞州期末) 用2，0，2，4这四个数进行如下运算，计算结果最大的式子是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024七上·新昌期末) 用计算器，按下列按键顺序输入则它表达的算式是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024七上·长春月考) 计算： $\text{[math]}$ ，这个运算应用了（）

A . 加法结合律 B . 乘法结合律 C . 乘法交换律 D . 分配律

答案解析收藏纠错 + 选题
4. (2024七上·裕华期末) 在计算 $\text{[math]}$ 时，有四位同学给出了以下四种计算步骤，其中正确的是（）

A . 原式 $\text{[math]}$ B . 原式 $\text{[math]}$ C . 原式 $\text{[math]}$ D . 原式 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023七上·应城期中) 已知有理数 $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . 0或2 C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022七下·万州期末) 某商场为促销对顾客实行优惠，规定：
（1）如一次性购物不超过200元，则不予优惠；
（2）如一次性购物超过200元，但不超过500元的，按标价给予9折优惠；
（3）如一次性购物超过500元的，其中500元按（2）给予优惠，超过500元的部分则给予8折优惠．
某人两次购物，分别付款160元与360元，如果他一次性购买这些商品，则应付（）

A . 468元 B . 498元 C . 504元 D . 520元

答案解析收藏纠错 + 选题
7. (2024七上·龙岗期末) 法国的“小九九”从“一一得一”到“五五二十五”和我国的“小九九”是一样的，后面的就改用手势了.下面两个图框是用法国“小九九”计算 $\text{[math]}$ 和 $\text{[math]}$ 的两个示例，且左手伸出的手指数不大于右手伸出的手指数.若用法国的“小九九”计算 $\text{[math]}$ ，左、右手依次伸出手指的个数是（）
$\text{[math]}$ ？

因为两手伸出的手指数的和为 $\text{[math]}$ ，未伸出的手指数的积为 $\text{[math]}$ ，所以 $\text{[math]}$
$\text{[math]}$ ？

因为两手伸出的手指数的和为 $\text{[math]}$ ，未伸出的手指数的积为 $\text{[math]}$ ，所以 $\text{[math]}$

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2016·绍兴)
我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”．如图，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数，由图可知，孩子自出生后的天数是（　　）

A . 84 B . 336 C . 510 D . 1326

答案解析收藏纠错 + 选题
9. (2022七上·黄岛期末) 九宫格起源于中国古代的神秘图案河图和洛书.如图，将 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 填入九宫格内，使每行、每列、每条对角线上三个数的和都相等，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022九上·铜梁开学考) 有一台特殊功能计算器，对任意两个整数只能完成求差后再取绝对值的运算，其运算过程是：输入第一个整数 $\text{[math]}$ ，只显示不运算，接着再输入整数 $\text{[math]}$ 后则显示 $\text{[math]}$ 的结果．比如依次输入1，2，则输出的结果是 $\text{[math]}$ ；此后每输入一个整数都是与前次显示的结果进行求差后再取绝对值的运算．有如下结论：①依次输入1，2，3，4，则最后输出的结果是2；②若将1，2，3，4这4个整数任意地一个一个输入，全部输入完毕后显示的结果的最大值是4；③若将1，2，3，4这4个整数任意地一个一个地输入，全部输入完毕后显示的结果的最小值是0；④若随意地一个一个地输入三个互不相等的正整数2， $\text{[math]}$ ， $\text{[math]}$ ，全部输入完毕后显示的最后结果设为 $\text{[math]}$ ，若 $\text{[math]}$ 的最大值为10，那么 $\text{[math]}$ 的最小值是6．上述结论中，正确的个数是 $\text{[math]}$ $\text{[math]}$

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

11. (2024·武威) 定义一种新运算*，规定运算法则为： $\text{[math]}$ * $\text{[math]}$ ( $\text{[math]}$ 均为整数，且 $\text{[math]}$ ).例： $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2024·温岭二模) 如图，教室后面储物柜上叠放了两堆共7个完全相同的生本教具，现测得叠放了3个数具的投高处离地两 $\text{[math]}$ ，叠放了4个教具的最高处离地面 $\text{[math]}$ ，若将7个教具叠成一堆放在柜子上，则最高处地面 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2024·北京市) 联欢会有A ， B ， C ， D四个节目需要彩排.所有演员到场后节目彩排开始.一个节目彩排完毕，下一个节目彩排立即开始.每个节目的演员人数和彩排时长（单位：min）如下：
节目
A
B
C
D
演员人数
10
2
10
1
彩排时长
30
10
20
10
已知每位演员只参演一个节目.一位演员的候场时间是指从第一个彩排的节目彩排开始到这位演员参演的节目彩排开始的时间间隔（不考虑换场时间等其他因素）.
若节目按“ $\text{[math]}$ ”的先后顺序彩排，则节目D的演员的候场时间为min；若使这23位演员的候场时间之和最小，则节目应按的先后顺序彩排

答案解析收藏纠错 + 选题
14. (2024·田阳模拟) 小明做了一个数字游戏：
第一步：取一个自然数 $\text{[math]}$ ，计算 $\text{[math]}$ 得 $\text{[math]}$ ；
第二步：算出 $\text{[math]}$ 的各位数字之和得 $\text{[math]}$ ，计算 $\text{[math]}$ 得 $\text{[math]}$ ；
第三步：算出 $\text{[math]}$ 的各位数字之和得 $\text{[math]}$ ，计算 $\text{[math]}$ 得 $\text{[math]}$ ；
以此类推， $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2023七上·平阳期中) 如图所示的程序图，当输入﹣1时，输出的结果是．

答案解析收藏纠错 + 选题
16. (2024七下·赫山开学考) 已知a与b的绝对值相同，符号相反，c与d互为倒数，m是表示到原点距离为5的数，n是最小正整数，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

三、计算题

17. (2024七上·黔东南期末) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2024七上·南关期末) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ；
3. （3） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2023七上·文山月考) 用简便方法计算：
1. （1） $\text{[math]}$ ；
2. （2）（99 $\text{[math]}$ ）×（-17）．
答案解析收藏纠错 + 选题

四、综合题

20. (2019七上·巴东期中) 运算律是解决许多数学问题的基础，在运算中有重要的作用，充分运用运算律能使计算简便高效.
例如：(－125 $\text{[math]}$ )÷(－5)

解：(－125 $\text{[math]}$ )÷(－5)=125 $\text{[math]}$ × $\text{[math]}$ =(125+ $\text{[math]}$ )× $\text{[math]}$ =125× $\text{[math]}$ + $\text{[math]}$ × $\text{[math]}$ =25+ $\text{[math]}$ =25 $\text{[math]}$
1. （1）计算：6÷(－ $\text{[math]}$ + $\text{[math]}$ )，A同学的计算过程如下：
  原式=6×(－ $\text{[math]}$ )+6× $\text{[math]}$ =－6+9=3.
  
  请你判断A同学的计算过程是否正确，若不正确，请你写出正确的计算过程.
2. （2）请你参考例题，用运算律简便计算(请写出具体的解题过程)：
  999×118 $\text{[math]}$ +333×(－ $\text{[math]}$ )－999×18 $\text{[math]}$ .
答案解析收藏纠错 + 选题
21. (2022七上·利川期末) 今年以来，由于受国际天然气形势的影响，我国天然气市场总体呈现量紧价高的态势，为确保天然气保供稳价，提高居民生活用气的保障，某地决定从今年 $\text{[math]}$ 月开始调整居民用气价格，调整前后价格如下表（每月用气量为 $\text{[math]}$ 立方米）：

用气类别

第一档（ $\text{[math]}$ ）
第二档（ $\text{[math]}$ ）
第三档（ $\text{[math]}$ ）
调整前
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
调整后
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
注：该地天然气收费按月实行阶梯收费
1. （1）某用户 $\text{[math]}$ 月（调整前）缴天然气费 $\text{[math]}$ 元，求该用户这月用气量；
2. （2）若该用户 $\text{[math]}$ 月（调整后）用气量与 $\text{[math]}$ 月相同，则该用户 $\text{[math]}$ 月比 $\text{[math]}$ 月多缴费多少元？
3. （3）因天气转冷，该用户今年 $\text{[math]}$ 月因取暖用气量急剧增加，缴天然气费 $\text{[math]}$ 元，该用户今年 $\text{[math]}$ 月用气量是多少立方米？
答案解析收藏纠错 + 选题
22. (2021七上·岚皋期末) 问题探索：如图，将一根木棒放在数轴（单位长度为1cm）上，木棒左端与数轴上的点A重合，右端与数轴上的点B重合.
1. （1）若将木棒沿数轴向右水平移动，则当它的左端移动到点B时，它的右端在数轴上所对应的数为30；若将木棒沿数轴向左水平移动，则当它的右端移动到点A时，它的左端在数轴上所对应的数为6，由此可得这根木棒的长为cm.
2. （2）图中点A所表示的数是，点B所表示的数是.
3. （3）实际应用：由（1）（2）的启发，请借助“数轴”这个工具解决下列问题：
  一天，妙妙去问奶奶的年龄，奶奶说：“我若是你现在这么大，你还要35年才出生；你若是我现在这么大，我就115岁啦! ”请问妙妙现在多少岁了？
答案解析收藏纠错 + 选题
23. (2022七上·晋州期中) 规定：求若干个相同的不为零的有理数的除法运算叫做除方．如 $\text{[math]}$ ， $\text{[math]}$ ．
类比有理数的乘方，我们把 $\text{[math]}$ 记作 $\text{[math]}$ ，读作“2的星3次方”；把 $\text{[math]}$ 记作 $\text{[math]}$ ，读作“ $\text{[math]}$ 的星4次方”．
一般地，把 $\text{[math]}$ 记作 $\text{[math]}$ （其中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为整数），读作“ $\text{[math]}$ 的星 $\text{[math]}$ 次方”．
1. （1）直接写出计算结果： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）结合（1）中的运算，尝试把有理数的除方运算转化为乘方运算，可以归纳如下：
  一个非零有理数的星 $\text{[math]}$ ， $\text{[math]}$ 为整数）次方等于（从以下四个选项中选择最合适的一个，填写序号即可）．
  ①这个数的相反数的 $\text{[math]}$ 次方；
  ②这个数的绝对值的 $\text{[math]}$ 次方；
  ③这个数的倒数的 $\text{[math]}$ 次方；
  ④这个数的 $\text{[math]}$ 次方．
3. （3）关于“除方”运算，下列说法错误的是____ ；
  
  A . 任何非零有理数的星3次方都等于它的倒数； B . 对于任何不小于3正整数 $\text{[math]}$ ， $\text{[math]}$ ； C . $\text{[math]}$ ； D . 负数的星5次方的结果是负数，负数的星6次方的结果是正数．
4. （4）结合上述探究结果，计算下式的值．
  $\text{[math]}$ ．
答案解析收藏纠错 + 选题
24. (2022七上·乐山期中) 找规律并计算：
1. （1）计算： $\text{[math]}$ =， $\text{[math]}$ =；
  $\text{[math]}$ =， $\text{[math]}$ =；
2. （2）猜想：观察上述式子可猜想出的结论是： $\text{[math]}$ =；
3. （3）试用你所猜想的结论计算：
  $\text{[math]}$ …… $\text{[math]}$ .
答案解析收藏纠错 + 选题
25. (2022七上·义乌月考) 概念学习：
现规定：求若干个相同的有理数（均不等于0）的商的运算叫做除方，比如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等，类比有理数的乘方，我们把2÷2÷2写作2^③ ，读作“2的圈3次方”，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）写作（﹣3）^④ ，读作“（﹣3）的圈4次方”，一般地把 $\text{[math]}$ （a≠0）写作a^ⓝ ，读作“a的圈n次方”．

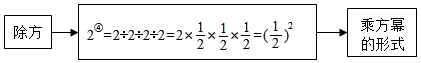
初步探究：
1. （1）直接写出计算结果：3^②＝；（﹣ $\text{[math]}$ ）^③＝；
2. （2）下列关于除方说法中，错误的有
  A．任何非零数的圈2次方都等于1
  
  B．任何非零数的圈3次方都等于它的倒数
  
  C．负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数
  
  D．圈n次方等于它本身的数是1或﹣1．
  深入思考：我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，那么有理数的除方运算如何转化为乘方运算呢？
3. （3）
  比较：（﹣2）^⑩（﹣4）^⑩；（填“＞”“＜”或“＝”）
4. （4）计算：﹣1^⑥+4²÷（﹣ $\text{[math]}$ ）^④×（﹣7）^③ ．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

苏科版(2024)数学七上2.7 有理数的混合运算同步练习

副标题：

*注意事项：

苏科版(2024)数学七上2.7 有理数的混合运算同步练习

试题分析

总体分析

题量分析

难度分析

知识点分析

	用气类别
	第一档（ $\text{[math]}$ ）	第二档（ $\text{[math]}$ ）	第三档（ $\text{[math]}$ ）
调整前	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
调整后	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

节目	A	B	C	D
演员人数	10	2	10	1
彩排时长	30	10	20	10

小学

初中

高中

苏科版(2024)数学七上2.7 有理数的混合运算 同步练习

副标题：

*注意事项：

苏科版(2024)数学七上2.7 有理数的混合运算 同步练习

试题分析

总体分析

题量分析

难度分析

知识点分析

苏科版(2024)数学七上2.7 有理数的混合运算同步练习

苏科版(2024)数学七上2.7 有理数的混合运算同步练习