1. (2022八上·城阳期中) 直角三角形三边满足两直角边的平方和等于斜边的平方，那么锐角三角形或钝角三角形的三边是否也满足这一关系呢？

1. （1） 情况一：锐角三角形

   如图①，在中，CD为斜边AB边上的高，在DC的延长线上取一点E，连接AE，BE，得到锐角三角形ABE，

   ∵ ，

   ∴ ．

   得出结论：锐角三角形夹锐角两边的平方和大于第三边的平方．

   像这种不用进行复杂的计算或推理，通过构造图形可以直观得到结论的方法，我们称之为“构图直观法”．

   

   情况二：钝角三角形

   你能借助上述“构图直观法”，得到钝角三角形三边之间类似的关系吗？请在图②中画出图形，得出结论并说明理由．得出结论：．

3. （2） 方法应用：

   下面我们用这种方法来研究其他问题：

   已知正方形ABCD，现作一个大正方形，使得正方形ABCD的四个顶点分别在大正方形的四条边上，则大正方形和正方形ABCD的面积之间会有怎样的数量关系？

   

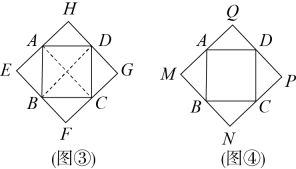
   如图③，作出一个满足要求的大正方形EFGH，使得正方形ABCD的四个顶点分别在大正方形各边中点上．过点A，B，C，D分别作大正方形的边的平行线，恰好与正方形ABCD的两条对角线所在直线重合，观察图形，则与的数量关系为：．

5. （3） 如图④，任意作出一个满足要求的大正方形MNPQ，若点A，B，C，D不是它各边中点，它的面积是否比图③中的正方形EFGH面积更大？请你利用上面介绍的“构图直观法”说明理由．
7. （4） 综上所述，满足要求的大正方形和正方形ABCD的面积之间的数量关系为：．