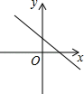
 B .
B . 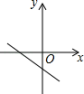 C .
C .  D .
D . 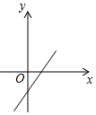







如图①,在中,CD为斜边AB边上的高,在DC的延长线上取一点E,连接AE,BE,得到锐角三角形ABE,
∵ ,
∴ .
得出结论:锐角三角形夹锐角两边的平方和大于第三边的平方.
像这种不用进行复杂的计算或推理,通过构造图形可以直观得到结论的方法,我们称之为“构图直观法”.

情况二:钝角三角形
你能借助上述“构图直观法”,得到钝角三角形三边之间类似的关系吗?请在图②中画出图形,得出结论并说明理由.得出结论:.
下面我们用这种方法来研究其他问题:
已知正方形ABCD,现作一个大正方形,使得正方形ABCD的四个顶点分别在大正方形的四条边上,则大正方形和正方形ABCD的面积之间会有怎样的数量关系?
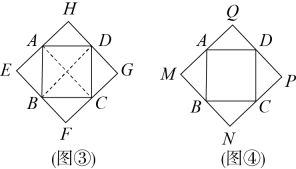
如图③,作出一个满足要求的大正方形EFGH,使得正方形ABCD的四个顶点分别在大正方形各边中点上.过点A,B,C,D分别作大正方形的边的平行线,恰好与正方形ABCD的两条对角线所在直线重合,观察图形,则与
的数量关系为:.

通过查阅资料知道伸缩缝是为大桥热胀冷缩而设置,并且大桥伸缩缝的长度主要受气温的影响,于是他对此进行了进一步的探究.在一年中他对当地某大桥伸缩缝的长度进行了五次测量,每次对伸缩缝长度测三次取其平均值,使测量结果更为精确,并将所测数据制成下表:
日期 | 气温t(℃) | 测量值l(mm) | |||
第一次 | 第二次 | 第三次 | 平均值 | ||
1月8日 | 2 | 79.3 | 79.4 | 79.4 | 79.4 |
2月16日 | 0 | 80.1 | 80.0 | 79.9 | 80.0 |
5月5日 | 11 | 76.8 | 76.7 | 77 | 76.8 |
8月1日 | 30 | 71.0 | 70.9 | 70.6 | 70.8 |
10月6日 | 22 | 73.6 | 73.1 | 73.6 | 73.4 |
根据上面的信息,小刚提出了4个问题,请你帮他解答:
