1. (2022七下·深圳月考) 如图，AB∥CD，定点E，F分别在直线AB，CD上，在平行线AB，CD之间有一动点P，满足0°<∠EPF<180° ．

1. （1） 试问∠AEP，∠EPF，∠PFC满足怎样的数量关系？

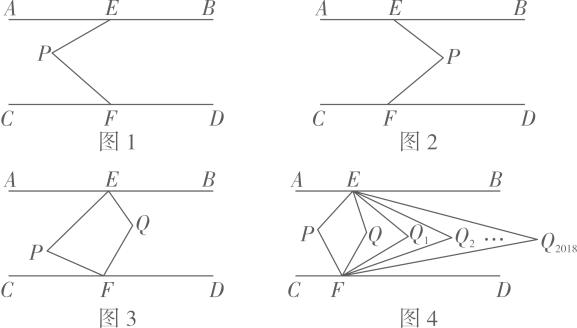
   解：由于点P是平行线AB， CD之间的一动点，因此需要对点P的位置进行分类讨论：

   如图1，当点P在EF的左侧时，∠AEP，∠EPF，∠PFC满足数量关系为

   如图2，当点P在EF的右侧时，∠AEP，∠EPF，∠PFC满足数量关系为

3. （2） 如图3，QE，QF分别平分∠PEB和∠PFD， 且点P在EF左侧．

   ①若∠EPF=60°，则∠EQF= ．

   ②猜想∠EPF与∠EQF的数量关系，并说明理由；

   ③如图4，若∠BEQ与∠DFQ的平分线交于点Q₁ ， ∠BEQ₁与∠DFQ₁的平分线交于点Q₂ ， ∠BEQ₂与∠DFQ₂的平分线交于点Q；依次类推，则∠EPF与∠EQ₂₀₁₈F满足怎样的数量关系？(直接写出结果)