广东省深圳市2021-2022学年第二学期学科素养形成七年级...

更新时间：2024-07-13 浏览次数：90 类型：月考试卷

一、选择题(共10小题，共30分)

1. (2022七下·深圳月考) 下列运算正确的是（）

A . (a-b)²=a²-b² B . (a³)²=a⁵ C . a⁵÷a³=a² D . a³+a²=a⁵

答案解析收藏纠错 + 选题
2. (2022七下·深圳月考) 科学家借助电子显微镜发现新型冠状病毒的平均直径约为0.000000125米，则数据0.000000125用科学记数法表示正确的是（）

A . 1.25×10⁸ B . 1.25×10^-8 C . 1.25×10⁷ D . 1.25×10^-7

答案解析收藏纠错 + 选题
3. (2022七下·深圳月考) 下列说法中，正确的是（）

A . 从直线外一点到这条直线的垂线段，叫做这个点到这条直线的距离 B . 平面内，互相垂直的两条直线不一定相交 C . 过一点有且只有一条直线垂直于已知直线 D . 直线AB外一点P与直线上各点连接而成的所有线段中最短线段的长是7cm，则点P到直线AB的距离是7cm

答案解析收藏纠错 + 选题
4. (2022七下·深圳月考) 如图，直线DE分别交射线BA，BG于点D，F，则下列条件中能判定DE∥BC的个数是（）

①∠ADE=∠GBC；②∠DFB=∠GBC；③∠EDB+∠ABC=180°；④∠GFE=∠GBC．

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
5. (2022七下·深圳月考) 如图，已知直线m∥n，线段AB的两个端点A，B分别落在直线m，n上，将线段AB绕点A按逆时针方向旋转80°得到线段AC，连接BC．若∠1=30°，则∠2的度数为（）

A . 15° B . 20° C . 25° D . 30°

答案解析收藏纠错 + 选题
6. (2022七下·深圳月考) 如图，点C在∠AOB的OB边上，用尺规作出了∠BCD=∠AOB．以下是排乱的作图过程：
①以点C为圆心，OE长为半径画 $\text{[math]}$ ，交OB于点M．②作射线CD，则∠BCD=∠AOB．③以点M为圆心，EF长为半径画弧，交 $\text{[math]}$ 于点D．④以点O为圆心，任意长为半径画 $\text{[math]}$ ，分别交OA，OB于点E，E则正确的作图顺序是（）

A . ①②③④ B . ③②④① C . ④①③② D . ④③①②

答案解析收藏纠错 + 选题
7. (2022七下·深圳月考) 已知(－x)(2x²－ax－1)－2x³＋3x²中不含x的二次项，则a的值是（）

A . 3 B . 2 C . -3 D . -2

答案解析收藏纠错 + 选题
8. (2022七下·深圳月考) 若a=0.3² ， b=-3^-2 ， c=( $\text{[math]}$ )^-2 ， d=( $\text{[math]}$ )⁰ ，则（）

A . a<b<c<d B . a<d<c<b C . b<a<d<c D . c<a<d<b

答案解析收藏纠错 + 选题
9. (2022七下·深圳月考) 长方形面积是3a²-3ab+6a，一边长为3a，则它的周长为（）

A . 2a-b+2 B . 8a-2b C . 8a-2b+4 D . 4a-b+2

答案解析收藏纠错 + 选题
10. (2022七下·深圳月考) 有若干个大小形状完全相同的小长方形，现将其中4个如图1摆放，构造出一个正方形，其中阴影部分面积为35；其中5个如图摆放，构造出一个长方形，其中阴影部分面积为102(各个小长方形之间不重叠、不留空)，则每个小长方形的面积为（）

A . 4 B . 8 C . 12 D . 16

答案解析收藏纠错 + 选题

二、填空题(每题3分，共15分)

11. (2022七下·深圳月考) 已知关于x，y的多项式x²-2kxy+16y是完全平方式，则k=

答案解析收藏纠错 + 选题
12. (2022七下·深圳月考) 若2x+3y-2=0，则9^x·27^y的值是.

答案解析收藏纠错 + 选题
13. (2022七下·深圳月考) 如图，已知EF⊥AB，∠1=26°，则当AB∥CD时，∠2=.

答案解析收藏纠错 + 选题
14. (2022七下·深圳月考) 如图，直线a∥b，三角尺(各角分别为：30°，60，90°)如图摆放，若∠1=52°，则∠2的度数为

答案解析收藏纠错 + 选题
15. (2022七下·深圳月考) 数学活动课上，小明同学尝试将正方形纸片剪去一个小正方形，剩余部分沿虚线剪开，拼成新的图形。现给出下列3种不同的剪、拼方案，其中能够验证平方差公式的方案是。(请填上正确的序号)

答案解析收藏纠错 + 选题

三、解答题(共55分)

16. (2022七下·深圳月考) 计算：已知(x+y)²=1，(x-y)²=49，求x²+y²和xy的值．

答案解析收藏纠错 + 选题
17. (2022七下·深圳月考) 阅读下列文字，并解决问题。
已知x²y=3，求2xy（x⁵y²-3x³y-4x）的值.
分析：考虑到满足x²y=3的x，y的可能值较多，不可以逐一代入求解，故考虑整体思想，将x²y=3整体代入.
解：2xy（x⁵y²-3x³y-4x）
=2x⁶y³-6x⁴y²-8x²y
=2（x²y）³-6（x²y）²-8x²y，
将x²y=3代入
原式=2×3³-6×3²-8×3=-24.
请你用上述方法解决下面问题：
已知ab=3，求（2a³b²-3a²b+4a）·（-2b）的值.

答案解析收藏纠错 + 选题
18. (2022七下·深圳月考) 如图，已知：CD平分∠ACB，AC∥DE，CD∥EF，求证：EF平分∠DEB．

证明：∵CD平分∠ACB (已知)，

∴∠DCA=∠DCE(角平分线的定义)．

∵AC∥DE (已知)，

∴∠DCA= ▲

∴∠DCE=∠CDE (等量代换) ．

∵CD∥EF(已知)，

∴ ▲ =∠CDE（），

∠DCE=∠BEF（），

∴ ▲ = ▲ (等量代换)，

∴EF平分∠DEB（）

答案解析收藏纠错 + 选题
19. (2022七下·深圳月考) 如图，∠AOB是花园内两条小路组成的角，点C在OA上，点D在OB上，现在过点C、点D分别建一条平行于 OB和OA的小路，请用尺规在图上画出它的位置．

答案解析收藏纠错 + 选题
20. (2022七下·深圳月考) 已知：如图， $\text{[math]}$ ， $\text{[math]}$ .
求证： $\text{[math]}$ ∥ $\text{[math]}$ .

答案解析收藏纠错 + 选题
21. 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了(a+b)ⁿ(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律．例如，在三角形中第三行的三个数1，2， 1，恰好对应(a+b)²=a²+2ab+b²展开式中的系数；第四行的四个数1，3，3，1，恰好对应着(a+b)³=a³+3a²b+3ab²+b³展开式中的系数等等．
1. （1）根据上面的规律，写出(a+b)⁵的展开式．
2. （2）利用上面的规律计算：2⁵-5×2⁴+10×2³-10×2²+5×2-1．
答案解析收藏纠错 + 选题
22. (2022七下·深圳月考) 阅读材料：
（1）1的任何次幂都为1；
（2）-1的奇数次幂为-1；
（3）-1的偶数次幂为1；
（4）任何不等于零的数的零次幂为1．
请问当x为何值时，代数式(2x+3)^x+2020的值为1．

答案解析收藏纠错 + 选题
23. (2022七下·深圳月考) 如图，AB∥CD，定点E，F分别在直线AB，CD上，在平行线AB，CD之间有一动点P，满足0°<∠EPF<180° ．
1. （1）试问∠AEP，∠EPF，∠PFC满足怎样的数量关系？
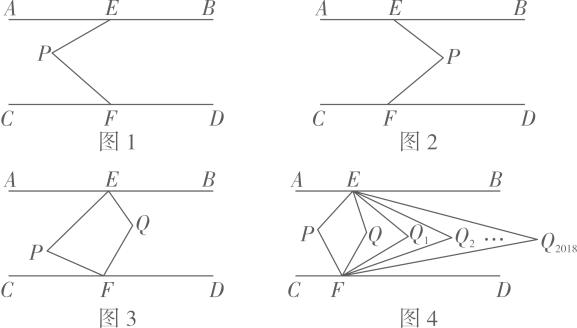
  解：由于点P是平行线AB， CD之间的一动点，因此需要对点P的位置进行分类讨论：
  
  如图1，当点P在EF的左侧时，∠AEP，∠EPF，∠PFC满足数量关系为
  
  如图2，当点P在EF的右侧时，∠AEP，∠EPF，∠PFC满足数量关系为
2. （2）如图3，QE，QF分别平分∠PEB和∠PFD，且点P在EF左侧．
  ①若∠EPF=60°，则∠EQF= ．
  
  ②猜想∠EPF与∠EQF的数量关系，并说明理由；
  
  ③如图4，若∠BEQ与∠DFQ的平分线交于点Q₁ ， ∠BEQ₁与∠DFQ₁的平分线交于点Q₂ ， ∠BEQ₂与∠DFQ₂的平分线交于点Q；依次类推，则∠EPF与∠EQ₂₀₁₈F满足怎样的数量关系？(直接写出结果)
答案解析收藏纠错 + 选题