课堂情境:数轴是规定了原点、正方向和单位长度的直线.任何有理数都可以用数轴上的点表示.数轴上表示一个数的点到原点的距离叫做这个数的绝对值.数轴上右边的数总比左边的数大…根据这些性质,我们可以借助数轴解决很多问题
今天我们研究数轴上两点之间的距离与这两个有理数之间的关系,
观察发现:
![]()
在数轴上,有理数与
对应的两点之间的距离为;
在数轴上,有理数与
对应的两点之间的距离为;
答疑解惑:
小明提出:在数轴上,有理数-4与-1对应的两点之间的距离可以写为吗?
小亮回答:不可以.两点之间的距离不能是负数.两个点之间的距离应该写成这两个数的差的绝对值;
小慧回答:不可以.两个点之间的距离等于右边的数减去左边的数
观察数轴上给出的两点之间距离,选用小亮或小慧的方法求数轴上两点之间距离;
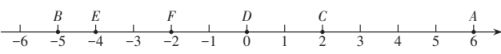
;
;
;
;
若点从点
出发以每秒2个单位长度的速度向左运动,同时点
从点
出发以每秒1个单位长度的速度向右运动,求经过多长时间
,
两点之间的距离为2个单位长度?