1. (2023八下·通州期中) 下面是小明设计的“作矩形ABCD”的尺规作图过程：

已知：在中，∠ABC＝90°．

求作：矩形ABCD ．

作法：如图，

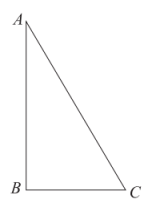
①分别以点A ， C为圆心、大于的长为半径作弧，两弧相交于E ， F两点；

②作直线EF ， 交AC于点P；

③连接BP并延长至点D ， 使得PD＝BP；

④连接AD ， CD ．

则四边形ABCD是矩形．

根据小明设计的尺规作图过程，解决以下问题：

1. （1） 使用直尺和圆规，补全图形（保留作图痕迹）；
3. （2） 完成下面的证明．

   证明：连接AE ， CE ， AF ， CF ．

   ∵AE＝CE ， AF＝CF ，

   ∴EF是线段AC的垂直平分线．

   ∴AP＝．

   又∵BP＝DP ，

   ∴四边形ABCD是平行四边形（填推理的依据）．

   ∵∠ABC＝90°，

   ∴四边形ABCD是矩形（填推理的依据）．