 B .
B .  C .
C .  D .
D . 

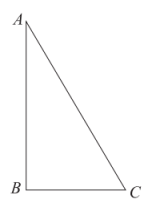
已知:在中,∠ABC=90°.
求作:矩形ABCD .
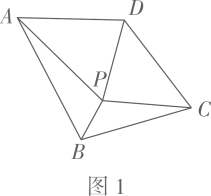
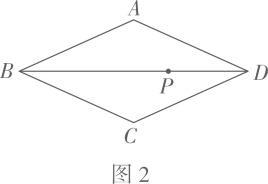
作法:如图,
①分别以点A , C为圆心、大于的长为半径作弧,两弧相交于E , F两点;
②作直线EF , 交AC于点P;
③连接BP并延长至点D , 使得PD=BP;
④连接AD , CD .
则四边形ABCD是矩形.
根据小明设计的尺规作图过程,解决以下问题:
证明:连接AE , CE , AF , CF .
∵AE=CE , AF=CF ,
∴EF是线段AC的垂直平分线.
∴AP=.
又∵BP=DP ,
∴四边形ABCD是平行四边形(填推理的依据).
∵∠ABC=90°,
∴四边形ABCD是矩形(填推理的依据).

①列表:下表是x与y的几组对应值,其中m=;
| x | … |
| | | | 0 | | 1 | 2 | 3 | … |
| y | … | 1 | | 2 | 3 | 4 | 3 | m | | 1 | … |
②描点:根据表中的数值描点 , 补充描出点
;
③连线:用平滑的曲线顺次连接各点,画出函数图象.
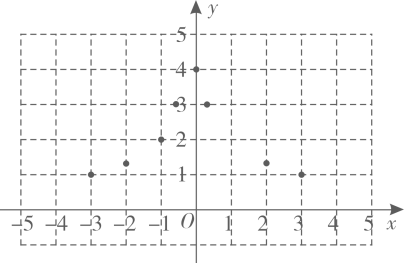
写出函数的一条性质:.
①观察你所画的函数图象,回答问题:若点 ,
为该函数图象上不同的两点,则
;
②根据函数图象,写出不等式的解集是.
②如果点P在函数的图象上,且为原点O关于坐标轴的“2倍距”,求b的取值范围.