运用“坐标法”解决几何问题
数学知识之间是相互联系的,有些几何问题可以运用“坐标法”解决.其步骤是:首先根据图形特点,在平面上建立坐标系,然后运用函数(或方程)知识研究几何图形,最后把图形性质用几何语言叙述,从而得到原先几何问题的答案.
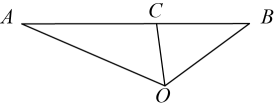
例题:如图,在中,
,
是
的角平分线,
,
, 用你所学的知识求线段
的长.
解:如图,以为坐标原点,
所在的直线为
轴,建立平面直角坐标系.
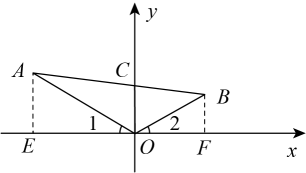
∵ ,
是
的角平分线,
∴ .
∴
∵ ,
,
∴ ,
,
,
.
∴ ,
设直线的函数表达式为
.
∴解得
.
∴
∴当时,
.
∴线段的长为3.
通过这个问题的解答,我们发现用“坐标法”解决几何问题,关键是根据图形特点,建立适当的坐标系.
任务:请用“坐标法”解答下面问题:
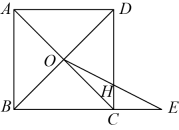
如图,已知正方形中,
, 点
在
的延长线上,且
, 连接
,
相交于点
, 连接
交
于点
, 求
的长.