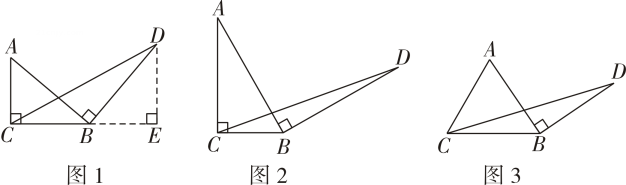
如图1,在等腰三角形ABC中,∠ACB=90°,BC=x,将边AB绕点B顺时针旋转90°得到线段BD,过点D作DE⊥CB交CB的延长线于点E,连接CD.则线段BC与DE的数量关系是,△BCD的面积为(用含x的式子表示);
如图2,在一般的Rt△ABC中,∠ACB=90°,BC=x,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,用含x的式子表示△BCD的面积,并说明理由.
如图3所示,在等腰三角形ABC中,AB=AC=5,将边AB绕点B顺时针旋转,当AB⊥BD,连接CD,若△BCD的面积为9,则CD的长为.