 B .
B .  C .
C .  D .
D . 

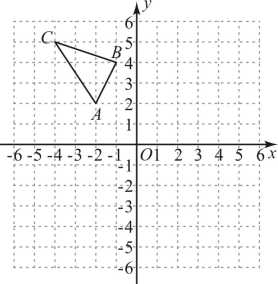
⑴若经过平移后得到
, 已知点
的坐标为
作出
并写出其余两个顶点的坐标;
⑵将绕点O按顺时针方向旋转
得到
, 作出
.
分解因式 .
解:设 , 则原式
.
这样的解题方法叫做“换元法”,即当复杂的多项式中某一部分重复出现时,我们用字母将其替换,从而简化这个多项式.换元法是一个重要的数学方法,不少问题能用换元法解决.
请你用“换元法”对下列多项式进行因式分解:
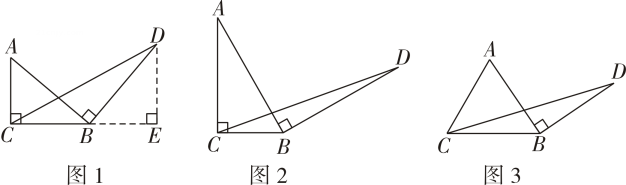
如图1,在等腰三角形ABC中,∠ACB=90°,BC=x,将边AB绕点B顺时针旋转90°得到线段BD,过点D作DE⊥CB交CB的延长线于点E,连接CD.则线段BC与DE的数量关系是,△BCD的面积为(用含x的式子表示);
如图2,在一般的Rt△ABC中,∠ACB=90°,BC=x,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,用含x的式子表示△BCD的面积,并说明理由.
如图3所示,在等腰三角形ABC中,AB=AC=5,将边AB绕点B顺时针旋转,当AB⊥BD,连接CD,若△BCD的面积为9,则CD的长为.