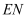有这样一个问题：如图1，在矩形中，，点E，F在对角线上，满足，点M，N分别在线段，上，连接，，，，设，当a取何值时，存在M、N，使得四边形是正方形？小宇为了解决这个问题，进行了如下探究，请补

当前位置：初中数学 / 解答题

1. (2024九上·海淀开学考) 有这样一个问题：
如图1，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ，点E，F在对角线 $\text{[math]}$ 上，满足 $\text{[math]}$ ，点M，N分别在线段 $\text{[math]}$ ， $\text{[math]}$ 上，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ ，当a取何值时，存在M、N，使得四边形 $\text{[math]}$ 是正方形？
小宇为了解决这个问题，进行了如下探究，请补充完整：
假设符合题意的正方形存在，
1. （1）画出示意图，如图2，由于四边形 $\text{[math]}$ 是正方形，那么它一定是平行四边形，由平行四边形的性质①______（填依据），可知 $\text{[math]}$ ，结合 $\text{[math]}$ 是矩形，可得 $\text{[math]}$ ，于是 $\text{[math]}$ ，因此，四边形 $\text{[math]}$ 的对角线交点恰好是 $\text{[math]}$ 的中点，如图3所示．
3. （2）在图3的基础上，由于 $\text{[math]}$ 是正方形，那么它还同时是菱形和矩形．于是由菱形的性质②______（填依据），可得 $\text{[math]}$ 于O，于是 $\text{[math]}$ 垂直平分 $\text{[math]}$ ；又由矩形的性质可得 $\text{[math]}$ ，这样就能够确定点E，F，M，N的位置了．
5. （3）根据（1）（2）的分析，在图4中作出正方形 $\text{[math]}$ （尺规作图，保留作图痕迹）；
7. （4）结合上述的探索，小宇发现符合题意的正方形 $\text{[math]}$ 是唯一的，此时a的值为______；
  解决问题后，小宇又有了进一步的思考：
9. （5）若将原问题改为：当a取何值时，存在M，N，使得四边形 $\text{[math]}$ 为矩形？请参照上面的思考，直接写出a的最小值．

微信扫码预览、分享更方便