1. (2016九上·怀柔期末) 在“解直角三角形”一章我们学习到“锐角的正弦、余弦、正切都是锐角的函数，统称为锐角三角函数” ．

小力根据学习函数的经验，对锐角的正弦函数进行了探究． 下面是小力的探究过程，请补充完成：

1. （1） 函数的定义是：“一般地，在一个变化的过程中，有两个变量x和y，对于变量x的每一个值，变量y都有唯一确定的值和它对应，我们就把x称为自变量，y称为因变量，y是x的函数”．由函数定义可知，锐角的正弦函数的自变量是，因变量是，自变量的取值范围是．
3. （2） 利用描点法画函数的图象． 小力先上网查到了整锐角的正弦值，如下：

   sin1°=0.01745240643728351    sin2°=0.03489949670250097    sin3°=0.05233595624294383

   sin4°=0.0697564737441253     sin5°=0.08715574274765816    sin6°=0.10452846326765346

   sin7°=0.12186934340514747    sin8°=0.13917310096006544    sin9°=0.15643446504023087

   sin10°=0.17364817766693033   sin11°=0.1908089953765448    sin12°=0.20791169081775931

   sin13°=0.22495105434386497 sin14°=0.24192189559966773 sin15°=0.25881904510252074

   sin16°=0.27563735581699916   sin17°=0.2923717047227367    sin18°=0.3090169943749474

   sin19°=0.3255681544571567    sin20°=0.3420201433256687    sin21°=0.35836794954530027

   sin22°=0.374606593415912     sin23°=0.3907311284892737    sin24°=0.40673664307580015

   sin25°=0.42261826174069944   sin26°=0.4383711467890774    sin27°=0.45399049973954675

   sin28°=0.4694715627858908    sin29°=0.48480962024633706   sin30°=0.5000000000000000

   sin31°=0.5150380749100542    sin32°=0.5299192642332049    sin33°=0.544639035015027

   sin34°=0.5591929034707468    sin35°=0.573576436351046     sin36°=0.5877852522924731

   sin37°=0.6018150231520483    sin38°=0.6156614753256583    sin39°=0.6293203910498375

   sin40°=0.6427876096865392 sin41°=0.6560590289905073 sin42°=0.6691306063588582

   sin43°=0.6819983600624985    sin44°=0.6946583704589972    sin45°=0.7071067811865475

   sin46°=0.7193398003386511 sin47°=0.7313537016191705 sin48°=0.7431448254773941

   sin49°=0.7547095802227719 sin50°=0.766044443118978 sin51°=0.7771459614569708

   sin52°=0.7880107536067219 sin53°=0.7986355100472928 sin54°=0.8090169943749474

   sin55°=0.8191520442889918    sin56°=0.8290375725550417    sin57°=0.8386705679454239

   sin58°=0.848048096156426 sin59°=0.8571673007021122 sin60°=0.8660254037844386

   sin61°=0.8746197071393957 sin62°=0.8829475928589269 sin63°=0.8910065241883678

   sin64°=0.898794046299167     sin65°=0.9063077870366499    sin66°=0.9135454576426009

   sin67°=0.9205048534524404 sin68°=0.9271838545667873 sin69°=0.9335804264972017

   sin70°=0.9396926207859083    sin71°=0.9455185755993167    sin72°=0.9510565162951535

   sin73°=0.9563047559630354    sin74°=0.9612616959383189    sin75°=0.9659258262890683

   sin76°=0.9702957262759965    sin77°=0.9743700647852352    sin78°=0.9781476007338057

   sin79°=0.981627183447664     sin80°=0.984807753012208     sin81°=0.9876883405951378

   sin82°=0.9902680687415704    sin83°=0.992546151641322     sin84°=0.9945218953682733

   sin85°=0.9961946980917455    sin86°=0.9975640502598242    sin87°=0.9986295347545738

   sin88°=0.9993908270190958    sin89°=0.9998476951563913   

   ①列表（小力选取了10对数值）；

   x

   …

   …

   y

   …

   …

   ②建立平面直角坐标系（两坐标轴可视数值需要分别选取不同长度做为单位长度）；

   ③描点．在平面直角坐标系xOy 中，描出了以上表中各对对应值为坐标的点；

   

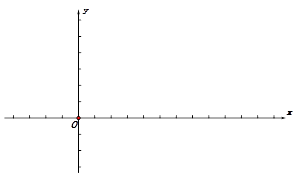
   ④连线． 根据描出的点，画出该函数的图象；

5. （3） 结合函数的图象，写出该函数的一条性质：．