
 B .
B .  C .
C .  D .
D . 
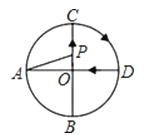
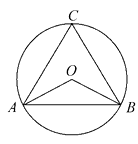
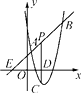
如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是( )
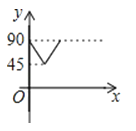 B .
B . 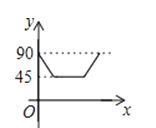 C .
C . 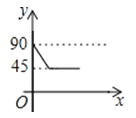 D .
D . 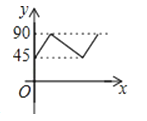
选手 | 甲 | 乙 | 丙 |
平均数 | 9.3 | 9.3 | 9.3 |
方差 | 0.026 | 0.015 | 0.032 |
则射击成绩最稳定的选手是.(填“甲”、“乙”、“丙”中的一个)
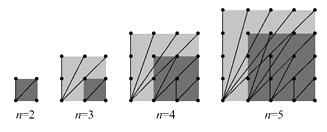
当n=2时,钉子板上所连不同线段的长度值只有1与 ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, ,2,
,2
五种,比n=2时增加了3种,即S=2+3=5.
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+() |
5×5 | () |
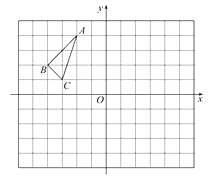
①将△ABC向右平移2个单位长度,作出平移后的△A1B1C1 , 并写出△A1B1C1各顶点的坐标.
②若将△ABC绕点(-1,0)顺时针旋转180°后得到△A2B2C2 , 并写出△A2B2C2各顶点的坐标.
③观察△A1B1C1和△A2B2C2 , 它们是否关于某点成中心对称?若是,请写出对称中心的坐标;若不是,说明理由.

分组 | 频数 | 频率 |
50.5~60.5 | 10 | a |
60.5~70.5 | b | |
70.5~80.5 | 0.2 | |
80.5~90.5 | 52 | 0.26 |
90.5~100.5 | 0.37 | |
合计 | c | 1 |
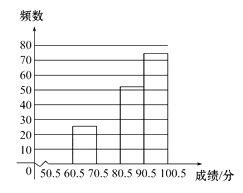
请根据以上提供的信息,解答下列问题:
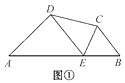
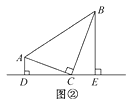
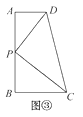
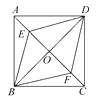
①请证明点P是四边形ABCD的边AB上的一个强相似点.
②若AD=3,BC=5,试求AB的长.