河南省信阳市2018届九年级数学中考一模试卷

更新时间：2018-09-10 浏览次数：514 类型：中考模拟

一、单选题、

1. (2018·信阳模拟) –2³的相反数是（）

A . –8 B . 8 C . –6 D . 6

答案解析收藏纠错 + 选题
2. (2018·信阳模拟) 碳纳米管的硬度与金刚石相当，却拥有良好的柔韧性，可以拉伸，我国某物理所研究组已研制出直径为0.5纳米的碳纳米管，1纳米=0.000000001米，则0.5纳米用科学记数法表示为（）

A . 0.5×10^–9米 B . 5×10^–8米 C . 5×10^–9米 D . 5×10^–10米

答案解析收藏纠错 + 选题
3. (2018·信阳模拟) 如图是一个几何体的三视图，则这个几何体是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2018·信阳模拟) 下列计算正确的是（）

A . a⁶÷a²=a³ B . a•a⁴=a⁴ C . （a³ ）⁴=a⁷ D . （﹣2a ）^﹣²= $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022九上·建始期中) 如图是边长为10 $\text{[math]}$ 的正方形铁片，过两个顶点剪掉一个三角形，以下四种剪法中，裁剪线长度所标的数据（单位： $\text{[math]}$ ）不正确的（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2018·信阳模拟) 某专卖店专营某品牌的衬衫，店主对上一周中不同尺码的衬衫销售情况统计如下：
尺码
39
40
41
42
43
平均每天销售数量/件
10
12
20
12
12
该店主决定本周进货时，增加一些41码的衬衫，影响该店主决策的统计量是（）

A . 平均数 B . 方差 C . 众数 D . 中位数

答案解析收藏纠错 + 选题
7. (2019八上·南山期中) 如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是（）

A . 乙前4秒行驶的路程为48米 B . 在0到8秒内甲的速度每秒增加4米/秒 C . 两车到第3秒时行驶的路程相等 D . 在4至8秒内甲的速度都大于乙的速度

答案解析收藏纠错 + 选题
8. (2018·信阳模拟)
如图，将矩形MNPQ放置在矩形ABCD中，使点M，N分别在AB，AD边上滑动，若MN=6，PN=4，在滑动过程中，点A与点P的距离AP的最大值为（　　）

A . 4 B . 2 $\text{[math]}$ C . 7 D . 8

答案解析收藏纠错 + 选题

二、填空题

9. (2018·信阳模拟) 分解因式：x²y–xy²=．

答案解析收藏纠错 + 选题
10. (2018·信阳模拟) 不等式组 $\text{[math]}$ 的最小整数解是．

答案解析收藏纠错 + 选题
11. (2018·信阳模拟) 如图，在已知的△ABC中，按以下步骤作图：
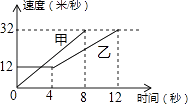
①分别以B，C为圆心，以大于 $\text{[math]}$ BC的长为半径作弧，两弧相交于两点M，N；②作直线MN交AB于点D，连接CD．若CD=AC，∠A=50°，则∠ACB=．

答案解析收藏纠错 + 选题
12. (2018·信阳模拟) 如图，在▱ABCD中，AD=2，AB=4，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是（结果保留π）．

答案解析收藏纠错 + 选题
13. (2018·信阳模拟) 如图，在矩形ABCD中，AB=8，AD=6，点E为AB上一点，AE=2 $\text{[math]}$ ，点F在AD上，将△AEF沿EF折叠，当折叠后点A的对应点A'恰好落在BC的垂直平分线上时，折痕EF的长为

答案解析收藏纠错 + 选题

三、解答题

14. (2018·信阳模拟) 化简并求值：（m+1）²+（m+1）（m﹣1），其中m是方程x²+x﹣1=0的一个根．

答案解析收藏纠错 + 选题
15. (2021七下·芜湖期末) 某中学初二年级抽取部分学生进行跳绳测试．并规定：每分钟跳90次以下的为不及格；每分钟跳90～99次的为及格；每分钟跳100～109次的为中等；每分钟跳110～119次的为良好；每分钟跳120次及以上的为优秀．测试结果整理绘制成如下两幅不完整的统计图．请根据图中信息，解答下列各题：
1. （1）参加这次跳绳测试的共有人；
2. （2）补全条形统计图；
3. （3）在扇形统计图中，“中等”部分所对应的圆心角的度数是；
4. （4）如果该校初二年级的总人数是480人，根据此统计数据，请你估算该校初二年级跳绳成绩为“优秀”的人数．
答案解析收藏纠错 + 选题
16. (2018·信阳模拟) 如图，AB是⊙O的弦，D为半径OA的中点，过D作CD⊥OA交弦AB于点E，交⊙O于点F，且CE=CB
1. （1）求证：BC是⊙O的切线；
2. （2）连接AF，BF，求∠ABF的度数．
答案解析收藏纠错 + 选题
17. (2018·信阳模拟) 共享单车被誉为“新四大发明”之一，如图1所示是某公司2017年向信阳市场提供一种共享自行车的实物图，车架档AC与CD的长分别为45cm，60cm，AC⊥CD，座杆CE的长为20cm，点A，C，E在同一条直线上，且∠CAB=75°，如图2．
1. （1）求车架档AD的长；
2. （2）求车座点E到车架档AB的距离．（结果精确到1cm，参考数据：sin75°=0.9659，cos75°=0.2588，tan75°=3.7321）
答案解析收藏纠错 + 选题
18. (2018·信阳模拟) 如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A，C分别在坐标轴上，点B的坐标为（4，2），直线y=– $\text{[math]}$ x+3交AB，BC于点M，N，反比例函数 $\text{[math]}$ 的图象经过点M，N．
1. （1）求反比例函数的解析式；
2. （2）若点P在x轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标．
答案解析收藏纠错 + 选题
19. (2018·信阳模拟) 某班为参加学校的大课间活动比赛，准备购进一批跳绳，已知2根A型跳绳和1根B型跳绳共需56元，1根A型跳绳和2根B型跳绳共需82元．
1. （1）求一根A型跳绳和一根B型跳绳的售价各是多少元？
2. （2）学校准备购进这两种型号的跳绳共50根，并且A型跳绳的数量不多于B型跳绳数量的3倍，请设计书最省钱的购买方案，并说明理由．
答案解析收藏纠错 + 选题
20. (2018·信阳模拟)
1. （1）问题发现：
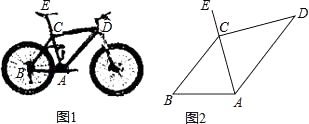
  如图1，在等边三角形ABC中，点M为BC边上异于B、C的一点，以AM为边作等边三角形AMN，连接CN，NC与AB的位置关系为；
2. （2）深入探究：
  如图2，在等腰三角形ABC中，BA=BC，点M为BC边上异于B、C的一点，以AM为边作等腰三角形AMN，使∠ABC=∠AMN，AM=MN，连接CN，试探究∠ABC与∠ACN的数量关系，并说明理由；
3. （3）拓展延伸：
  如图3，在正方形ADBC中，AD=AC，点M为BC边上异于B、C的一点，以AM为边作正方形AMEF，点N为正方形AMEF的中点，连接CN，若BC=10，CN= $\text{[math]}$ ，试求EF的长．
答案解析收藏纠错 + 选题
21. (2018·信阳模拟) 如图，在矩形OABC中，点O为原点，边OA的长度为8，对角线AC=10，抛物线y= $\text{[math]}$ x²+bx+c经过点A、C，与AB交于点D．
1. （1）求抛物线的函数解析式；
2. （2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ=CP，连接PQ，设CP=m，△CPQ的面积为S．
  ①求S关于m的函数表达式并求出S最大时的m值；
  ②在S最大的情况下，在抛物线y= $\text{[math]}$ x²+bx+c的对称轴上，若存在点F，使△DFQ为直角三角形，请直接写出所有符合条件的点F的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题