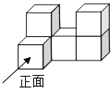
如图,在△ABC中,AD是中线,DE⊥BC交AB于E,AH∥DE交BC于H,且∠DAH=∠CAH,连接CE交AD于F,交AH于G.下列结论:①△AEF∽△CEA;②FH∥AC;③若CE⊥AB,则tan∠BAC=2;④若四边形AEDG是菱形,则∠ACB=60°.其中正确的是( )

如图,已知点A,C在反比例函数y= (a>0)的图像上,点B,D在反比例函数y=
(b<0)的图像上,AB∥CD∥y轴,AB,CD在y轴的同侧,AB=3,CD=2,AB与CD的距离为1,则a﹣b的值是.



项目选择情况统计图训练后篮球定时定点投篮测试进球数统计表
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |

请你根据图表中的信息回答下列问题:
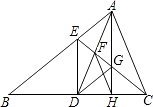
【探究1】如图1,正方形ABCD为“绣湖四边形”,BE⊥l于点E,BE的反向延长线交直线k于点F.求正方形ABCD的边长.

【探究3】如图2,菱形ABCD为“绣湖四边形”且∠ADC=60°,△AEF是等边三角形,AE⊥k于点E,∠AFD=90°,直线DF分别交直线l、k于点G、M.求证:EC=DF.

【拓展】如图3,l∥k,等边三角形ABC的顶点A、B分别落在直线l、k上,AB⊥k于点B,且AB=4,∠ACD=90°,直线CD分别交直线l、k于点G、M,点D、E分别是线段GM、BM上的动点,且始终保持AD=AE,DH⊥l于点H.猜想:DH在什么范围内,BC∥DE?并说明此时BC∥DE的理由.

如图,二次函数y=﹣x2+ x+4与x轴交于A、B两点,与y轴交于点C,点P从点O出发沿OA以每秒1个单位长度的速度向点A运动,到达点A后立刻在以原来的速度沿AO返回;点Q从点A出发沿AC以每秒1个单位长度的速度向点C匀速运动,过点Q作QD⊥x轴,垂足为D.点P、Q同时出发,当点Q到达点C时停止运动,点P也随之停止.设点P,Q的运动时间为t(t≥0).
