放在足够长的木板上的物体A和B由同种材料制成,且表面粗糙程度一样,现随长木板以速度v向右做匀速直线运动,如图所示.某时刻木板突然停止运动,已知mA>mB , 下列说法正确的是( )
![]()
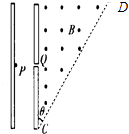
在匀强电场中有一个半径为R=1m的圆,电场方向与圆的平面平行,O,P两点电势差为10V,一个电子在该匀强电场中仅受电场力作用下运动,且在P,Q两点上速度方向与圆的切线一致,速度大小均为1m/s,则( )

如图所示,小物块以初速度v0从O点沿斜面向上运动,同时从O点斜向上抛出一个速度大小也为v0的小球,物块和小球在斜面上的P点相遇.已知物块和小球质量相等,空气阻力忽略不计,则( )

如图所示,平行板电容器两极板水平放置,电容为C,开始时开关闭合,电容器与一直流电源相连,极板间电压为U,两极板间距为d,电容器储存的能量E= .一电荷量为﹣q的带电油滴,以初动能Ek0从平行板电容器的两个极板中央水平射入(极板足够长),带电油滴恰能沿图中所示水平虚线匀速通过电容器,则( )

某学习小组做探究向心力与向心加速度关系实验.实验装置如图甲:一轻质细线上端固定在拉力传感器O点,下端悬挂一质量为m的小钢球.小球从A点静止释放后绕O点在竖直面内沿着圆弧ABC摆动.已知重力加速度为g,主要实验步骤如下:

①用游标卡尺测出小球直径d;
②按图甲所示把实验器材安装调节好.当小球静止时,如图乙所示,毫米刻度尺0刻度与悬点O水平对齐(图中未画出),测得悬点O到球心的距离L=m;
③利用拉力传感器和计算机,描绘出小球运动过程中细线拉力大小随时间变化的图线,如图丙所示.
④利用光电计时器(图中未画出)测出小球经过B点过程中,其直径的遮光时间为△t;
可得小球经过B点瞬时速度为v=(用d、△t表示).
⑤若向心力与向心加速度关系遵循牛顿第二定律,则小球通过B点时物理量m、v、L、g、F1(或F2)应满足的关系式为:.
某同学用如图所示电路进行实验,测定电源电动势、电压表内阻及电流表量程.器材如下:
电源E(电动势大小、内阻未知);
电流表 ![]() (总刻度30小格,量程未知);
(总刻度30小格,量程未知);
电阻箱R(0﹣9999.9Ω);
电压表 ![]() (0﹣3V);
(0﹣3V);
单刀双掷开关S,及导线若干.
实验步骤如下:
a.单刀双掷开关S接1,调节电阻箱阻值,使电流表满偏(指针偏转30格),读出此时电阻箱阻值为800.0Ω.
b.继续调节电阻箱阻值,当电流表半偏(指针偏转15格)时,读出电阻箱阻值为1800.0Ω.
c.开关S接2,把电阻箱阻值调为0,读出此时电流表指针偏转10格,电压表示数2.80V.
请回答下列问题:

如图甲所示是一台打桩机的简易模型,重锤A在绳拉力F作用下从桩B处由静止开始运动,上升一段高度后撤去F,重锤继续运动到最高点后自由下落,落回桩处,将桩打入一定深度.已知重锤的质量m=42kg,重锤上升过程中,动能EK与上升高度h的关系图像如图乙所示.不计一切摩擦,g取10m/s2 . 求: 
如图甲所示,与水平面成θ角的两根足够长的平行绝缘导轨,间距为L,导轨间有垂直导轨平面方向、等距离间隔的匀强磁场B1和B2 , B1和B2的方向相反,大小相等,即B1=B2=B;导轨上有一质量为m的矩形金属框abcd,其总电阻为R,框的宽度ab与磁场间隔相同,框与导轨间动摩擦因数为µ;开始时,金属框静止不动,重力加速度为g;

一定质量的理想气体经历了如图所示的A→B→C→D→A循环,该过程每个状态视为平衡态,各状态参数如图所示.A状态的压强为1×105Pa,求:
(i)B状态的温度;
(ii)完成一个循环,气体与外界热交换的热量.


(i)玻璃对该单色光的折射率;
(ii)该单色光通过玻璃圆柱体的最长时间.
如图所示,ABC是光滑轨道,BC段水平,C端固定一重锤线,重锤正下方为O点,在轨道上固定一挡板D,从贴紧挡板D处由静止释放质量为m1小球1,小球1落在M点,测得M点与O点距离2l.在C的末端放置一个大小与小球1相同的小球2,其质量为m2;现仍从D处静止释放小球1,小球1与小球2发生正碰,小球2落在N点,小球1落在P点,测得OP为l,ON为3l;求
(i)小球1与小球2的质量之比 ;
(ii)试通过计算判断两球的碰撞是否完全弹性碰撞.
