人教版九年级数学上册第二十五章概率初步单元检测a卷

更新时间：2018-10-31 浏览次数：359 类型：单元试卷

一、选择题

1. 下列事件是必然事件的是（）

A . 打开电视机，正在播放动画片 B . 2018年世界杯德国队一定能夺得冠军 C . 某彩票中奖率是1%，买100张一定会中奖 D . 投掷一枚普通的正方体骰子，连续投掷3次，出现的点数之和不可能等于19

答案解析收藏纠错 + 选题
2. 一个布袋里装有2个红球，3个黑球，4个白球，它们除颜色外都相同，从中任意摸出1个球，则下列事件中，发生可能性最大的是（）

A . 摸出的是白球 B . 摸出的是黑球 C . 摸出的是红球 D . 摸出的是绿球

答案解析收藏纠错 + 选题
3. (2023八下·宿迁期末) 标号为A、B、C、D的四个盒子中所装有的白球和黑球数如下，则下列盒子最易摸到黑球的是（）

A . 12个黑球和4个白球 B . 10个黑球和10个白球 C . 4个黑球和2个白球 D . 10个黑球和5个白球

答案解析收藏纠错 + 选题
4. 小明做了6次掷质地均匀硬币的试验，在前 5 次试验中，有 2 次正面朝上，3 次正面朝下，那么第 6 次试验，硬币正面朝上的概率是（）

A . 1 B . 0 C . 0.5 D . 不稳定

答案解析收藏纠错 + 选题
5. 下列说法不正确的是（）

A . 把4个球放入三个抽屉中，其中至少一个抽屉中有2个球时必然事件 B . 数据1，2，2，3的平均数是2 C . 数据5，﹣2，﹣3，0的方差是0 D . 如果某种游戏活动的中奖率为40%，那么参加这种活动10次不一定有4次中奖

答案解析收藏纠错 + 选题
6. 如图，在2×2的正方形网格中有9个格点，已经取定点A和B，在余下的7个点中任取一点C，使△ABC为直角三角形的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. 如图，在3×3的方格中，点A、B、C、D、E、F都是格点，从A、D、E、F四点中任意取一点，以所取点及B、C为顶点画三角形，所画三角形是直角三角形的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021九上·太原期中) 不透明的袋子中装有红球1个、绿球1个、白球2个，除颜色外无其他差别．随机摸出一个小球后不放回，再摸出一个球，则两次都摸到白球的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022九上·温州开学考) 一个不透明的袋中有四张完全相同的卡片，把它们分别标上数字1、2、3、4．随机抽取一张卡片，然后放回，再随机抽取一张卡片，则两次抽取的卡片上数字之积为偶数的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. 学校团委在“五四”青年节举行“校园之星”颁奖活动中，九（1）班决定从甲、乙、丙、丁四人中随机派两名代表参加此活动，则所选两名代表恰好是甲和乙的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. 在一个不透明的袋子中装有仅颜色不同的5个小球，其中红球3个，黑球2个，先从袋中取出m（m≥1）个红球，不放回，再从袋子中随机摸出1个球．将“摸出黑球”记为事件A．
1. （1）若A为必然事件，则m的值为；
2. （2）若A发生的概率为 $\text{[math]}$ ，则m的值为．
答案解析收藏纠错 + 选题
12. 如图，是可以自由转动的一个转盘，转动这个转盘，当它停下时，指针落在标有号码上的可能性最大．

答案解析收藏纠错 + 选题
13. 小华抛一枚硬币10次，只有2次正面朝上，当他抛第11次时，正面朝上的概率是．

答案解析收藏纠错 + 选题
14. 一个不透明的口袋中有5个红色小球和3个黄色小球，每个小球除颜色外其他都相同．现从中随机摸出一个小球，设摸到红色小球的概率是P（红），摸到黄色小球的概率是P（黄），则它们的大小关系是：P（红）P（黄）．（用“=”、“＞“或“＜“填空）

答案解析收藏纠错 + 选题
15. (2021·普陀模拟) 某校组织“优质课大赛”活动，经过评比有两名男教师和两名女教师获得一等奖，学校将从这四名教师中随机挑选两位教师参加市教育局组织的决赛，挑选的两位教师恰好是一男一女的概率为．

答案解析收藏纠错 + 选题
16. 小明和小红玩抛硬币游戏，连续抛两次，小明说：“如果两次都是正面，那么你赢；如果两次是一正一反，则我嬴．”小红赢的概率是，据此判断该游戏（填“公平”或“不公平”）．

答案解析收藏纠错 + 选题

三、解答题

17. 某校九年级（1）班的一个数学学习小组对全班某次测试中的“一道满分值为6分的解答题得分”情况进行了统计，绘制成下列不完整的统计图（学生得分均为整数）：

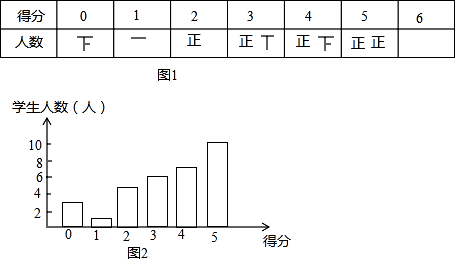
已知全班同学此题的平均得分为4分，结合表格解决下列问题：
1. （1）完成表格，并求该班学生总数；
2. （2）根据表中提供的数据，补全条形统计图；并判断下列说法中正确的有．（填序号即可）
  ①该班此题得分的众数是6；
  
  ②“随机抽取该班一份试卷，此题得1分”是不可能事件；
  
  ③该班学生此题得分的中位数是4；
  
  ④若将“该班同学本道题的得分情况”绘制成扇形统计图，求“此题得0分”的人数所对应的圆心角的度数为36°；
3. （3）若本年级学生共有540人，请你估计整个年级中此题得满分的学生人数．
答案解析收藏纠错 + 选题
18. 从一副扑克牌中任意抽取一张，①这张牌是“A”；②这张牌是“红心的”；③这张牌是“大王”；④这张牌是“红色的”。
估计上述事件发生的可能性的大小，将这些事件的序号按发生的可能性从小到大的顺序排列．

答案解析收藏纠错 + 选题
19. 中央电视台“幸运 52”栏目中的“百宝箱”互动环节，是一种竞猜游戏，游戏规则如下：在20个商标牌中，有5个商标牌的背面注明一定的奖金额，其余商标牌的背面是一张哭脸，若翻到哭脸，就不得奖，参与这个游戏的观众有三次翻牌机会（翻过的牌不能再翻）．某观众前两次翻牌均获得若干奖金，那么他第三次翻牌获奖的概率是多少？

答案解析收藏纠错 + 选题
20. 一个不透明的袋中装有5个黄球、15个黑球和20个红球，它们出颜色外都相同．
1. （1）求从袋中摸出一个球是黄球的概率；
2. （2）现从袋中取出若干个黑球，并放入相同数量的黄球，搅拌均匀后，使从袋中摸出一个球是黄球的概率是 $\text{[math]}$ ，问取出了多少个黑球？
答案解析收藏纠错 + 选题
21. 一个不透明的口袋中装有4张卡片，卡片上分別标有数字1、﹣2、3、﹣4，这些卡片除数字外都相同．王兴从口袋中随机抽取一张卡片，钟华从剩余的三张卡片中随机抽取一张，求两张卡片上数字之积．
1. （1）请你用画树状图或列表的方法，列出两人抽到的数字之积所有可能的结果．
2. （2）求两人抽到的数字之积为正数的概率．
答案解析收藏纠错 + 选题
22. 小亮和小芳都想参加学校杜团组织的暑假实践活动，但只有一个名额，小亮提议用如下的办法决定谁去等加活动：将一个转盘9等分，分别标上1至9九个号码，随意转动转盘，若转到2的倍数，小亮去参加活动；转到3的倍数，小芳去参加活动；转到其它号码则重新特动转盘．
1. （1）转盘转到2的倍数的概率是多少？
2. （2）你认为这个游戏公平吗？请说明理由．
答案解析收藏纠错 + 选题
23. 随机掷一枚图钉，落地后只能出现两种情况：“钉尖朝上”和“钉尖朝下”．这两种情况的可能性一样大吗？
1. （1）求真小组的同学们进行了实验，并将实验数据汇总填入下表．请补全表格：
  ①，②，③.
  试验总次数n
  20
  40
  80
  120
  160
  200
  240
  280
  320
  360
  400
  “钉尖朝上”的次数 m
  4
  12
  32
  60
  100
  140
  156
  196
  200
  216
  248
  “钉尖朝上”m的频率n
  0.2
  0.3
  0.4
  0.5
  0.625
  0.7
  0.65
  0.7
  ①
  ②
  ③
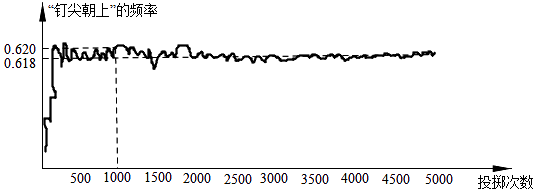
2. （2）为了加大试验的次数，老师用计算机进行了模拟试验，将试验数据制成如图所示的折线图．据此，同学们得出三个推断：
  ①当投掷次数是500时，计算机记录“钉尖朝上”的次数是308，所以“钉尖朝上”的概率是0.616；
  ②随着试验次数的增加，“钉尖朝上”的频率在0.618附近摆动，显示出一定的稳定性，据此估计“钉尖朝上”的概率是0.618；
  ③若再次用计算机模拟实验，当投掷次数为1000时，则“钉尖朝上”的次数一定是620次．
  其中合理的是．
3. （3）向善小组的同学们也做了1000次掷图钉的试验，其中640次“钉尖朝上”．据此，他们认为“钉尖朝上”的可能性比“钉尖朝下”的可能性大．你赞成他们的说法吗？请说出你的理由．
答案解析收藏纠错 + 选题
24. 在课堂上，老师将除颜色外都相同的1个黑球和若干个白球放入一个不透明的口袋并搅匀，让全班同学依次进行摸球试验，每次随机摸出一个球，记下颜色再放回搅匀，下表是试验得到的一组数据．
摸球的次数n
100
150
200
500
800
摸到黑球的次数m
26
37
49
124
200
摸到黑球的频率 $\text{[math]}$
0.26
0.247
0.245
0.248
a
1. （1）表中a的值等于；
2. （2）估算口袋中白球的个数；
3. （3）用画树状图或列表的方法计算连续两名同学都摸出白球的概率．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

人教版九年级数学上册第二十五章概率初步单元检测a卷

副标题：

*注意事项：

人教版九年级数学上册第二十五章概率初步单元检测a卷

试题分析

总体分析

题量分析

难度分析

知识点分析

试验总次数n	20	40	80	120	160	200	240	280	320	360	400
“钉尖朝上”的次数 m	4	12	32	60	100	140	156	196	200	216	248
“钉尖朝上”m的频率n	0.2	0.3	0.4	0.5	0.625	0.7	0.65	0.7	①	②	③

摸球的次数n	100	150	200	500	800
摸到黑球的次数m	26	37	49	124	200
摸到黑球的频率 $\text{[math]}$	0.26	0.247	0.245	0.248	a

小学

初中

高中

人教版九年级数学上册 第二十五章概率初步 单元检测a卷

副标题：

*注意事项：

人教版九年级数学上册 第二十五章概率初步 单元检测a卷

试题分析

总体分析

题量分析

难度分析

知识点分析

人教版九年级数学上册第二十五章概率初步单元检测a卷

人教版九年级数学上册第二十五章概率初步单元检测a卷