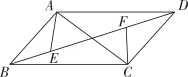
B .
B .  C .
C .  D .
D . 





第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
由此可知,由纸片拼成的五边形PMQRN中,对角线MN长度的最小值为.


①根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图象.
②观察函数图象,当时,y的值为多少?当y的值最大时,x的值为多少? ▲ , ▲ .
结合函数图象,写出该函数的两条性质或结论.
x(h) | … | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | … |
y(cm) | … | 189 | 137 | 103 | 80 | 101 | 133 | 202 | 260 | … |
当潮水高度超过260 , 货轮能安全进出港口.问当天货轮进出港口最佳时间段?
中小学生每周参加家庭劳动时间x(h)分为5组:第一组(0≤x<0.5),第二组(0.5≤x<1),第三组(1≤x<1.5),第四组(1.5≤x<2),第五组(x≥2).根据以上信息,解答下列问题:


.
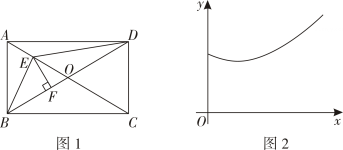
①证明 , 并求出在(1)条件下
的值;
②连接 , 求
周长的最小值;
①若 , 则方程
必有一个根为1;
②若方程有两个不相等的实根,则方程
必有两个不相等的实根;
③若是方程
的一个根,则一定有
成立;
④若是一元二次方程
的根,则
.
其中正确的有( )