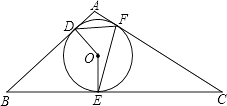
B .
B .  C .
C .  D .
D . 
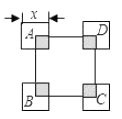
 B .
B .  C .
C . 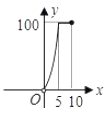 D .
D . 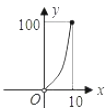
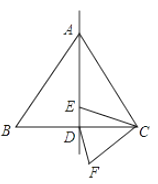
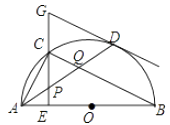

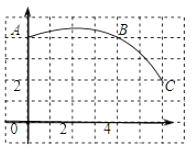
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④若点A(一3,yl)、点B(- ,y2)、点C(
,y3)在该函数图象上,则yl<y3<y2;⑤若方程a(x+1)(x-5)=-3的两根为x1和x2 , 且x1<x2 , 则x1<-1<5<x2 . 其中正确的结论有 (只需填写序号)
②请画出△ABC关于原点O成中心对称的图形△A2B2C2;