2018-2019学年初中数学华师大版八年级下册17.2.1...

更新时间：2019-04-10 浏览次数：245 类型：同步测试

一、选择题

1. 根据下列表述，能确定具体位置的是（）

A . 某电影院2排 B . 大桥南路 C . 北偏东30° D . 东经108°，北纬43°

答案解析收藏纠错 + 选题
2. 一个有序数对可以（）

A . 确定一个点的位置 B . 确定两个点的位置 C . 确定一个或两个点的位置 D . 不能确定点的位置

答案解析收藏纠错 + 选题
3. (2024七下·惠州期中) 如果电影票上的“5排2号”记作（5，2），那么（4，3）表示（）

A . 3排5号 B . 5排3号 C . 4排3号 D . 3排4号

答案解析收藏纠错 + 选题
4. 已知点 $\text{[math]}$ 不在第一象限，则点 $\text{[math]}$ 在（）

A . x轴正半轴上 B . x轴负半轴上 C . y轴正半轴上 D . y轴负半轴上

答案解析收藏纠错 + 选题
5. (2020八上·新昌月考) 如图，笑脸盖住的点的坐标可能为（）

A . (－2，3) B . (3，－4) C . (－4，－6) D . (5，2)

答案解析收藏纠错 + 选题
6. (2020八上·辽阳期中) 甲、乙两名同学下棋，甲执圆子，乙执方子.如图，棋盘中心方子的位置用（－1，0）表示，右下角方子的位置用（0，－1）表示，甲将第4枚圆子放入棋盘后，所有棋子构成一个轴对称图形，甲放的位置是（）

A . （－2，1） B . （－1，1） C . （－1，0） D . （－1，2）

答案解析收藏纠错 + 选题
7. 已知点P（a+5，9+a）位于二象限的角平分线上，则a的值为（）

A . 3 B . -3 C . -7 D . -1

答案解析收藏纠错 + 选题
8. (2021八上·诸暨月考) 已知点A(4，2)，B(-2，2)，则直线AB ( )

A . 平行于x轴 B . 平行于y轴 C . 经过原点 D . 以上都有可能

答案解析收藏纠错 + 选题
9. 点A（a + 1，a）关于x轴对称的点在第一象限，则a的取值范围是（）

A . -1< a < 0 B . $\text{[math]}$ C . D .

答案解析收藏纠错 + 选题
10. (2021七下·爱辉期末) 如图，动点P在平面直角坐标系中按图中箭头所示的方向运动，第1次从原点运动到（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过2017次运动后，动点P的坐标为（）

A . （2017，1） B . （2017，0） C . （2017，2） D . （2016，0）

答案解析收藏纠错 + 选题

二、填空题

11. 在我们生活中通常用两种方法来确定物体的位置．如小岛A在码头O的南偏东60°方向的14千米处，若以码头O为坐标原点，正东方向为x轴的正方向，正北方向为y轴的正方向，1千米为单位长度建立平面直角坐标系，则小岛A也可表示成．

答案解析收藏纠错 + 选题
12. 点P（1，－2）关于x轴对称的点的坐标是．

答案解析收藏纠错 + 选题
13. (2019七下·许昌期末) 点P在第二象限，到x轴距离为3，到y轴距离为2，点P坐标。

答案解析收藏纠错 + 选题
14. 已知点A（－2，0），B（3，0），点C在y轴上，且S_三角形_ABC＝10，则点C的坐标为．

答案解析收藏纠错 + 选题
15. 某人从A点出发，向北偏东60°方向走了10米到达B点，再从B点向南偏西15°方向走了10米到达c点，则∠ABC等于。

答案解析收藏纠错 + 选题
16. 如图所示，线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的长度分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ 平分 $\text{[math]}$ .若将 $\text{[math]}$ 点表示为 $\text{[math]}$ ，点 $\text{[math]}$ 表示为 $\text{[math]}$ ，则 $\text{[math]}$ 点可表示为.

答案解析收藏纠错 + 选题
17. 已知点A（2，4）与点B（b-1，2a）关于原点对称，则ab=．

答案解析收藏纠错 + 选题

三、解答题

18. 已知A(a－3，a²－4)，求a的值及点A的坐标．
1. （1）当点A在x轴上；
2. （2）当点A在y轴上．
答案解析收藏纠错 + 选题
19. 已知点 $\text{[math]}$ 在第三象限．
1. （1）化简 $\text{[math]}$ ．
2. （2）点 $\text{[math]}$ 到 $\text{[math]}$ 轴的距离是到 $\text{[math]}$ 轴的 $\text{[math]}$ 倍，请求出 $\text{[math]}$ 点坐标．
答案解析收藏纠错 + 选题
20. 如图，方格纸中每个小方格都是边长为1个单位的正方形，若学校位置坐标为A（2，1），图书馆位置坐标为B（﹣1，﹣2），解答以下问题：
1. （1） ①在图中标出平面直角坐标系的原点，并建立直角坐标系；
  ②若体育馆位置坐标为C（1，﹣3），请在坐标系中标出体育馆的位置；
2. （2）顺次连接学校、图书馆、体育馆，得到△ABC，求△ABC的面积．
答案解析收藏纠错 + 选题
21. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（﹣4，5），（﹣1，3）．
1. （1） ①请在如图所示的网格平面内作出平面直角坐标系；
  ②请作出△ABC关于y轴对称的△A₁B₁C₁；
2. （2）写出点B₁的坐标；
3. （3）求△ABC的面积．
答案解析收藏纠错 + 选题
22. 在平面直角坐标系中（单位长度为1cm），已知点M （m，0），N （n，0），且 $\text{[math]}$ ＋|2m＋n|＝0．
1. （1）求m，n的值；
2. （2）若点E是第一象限内一点，且EN⊥x轴，点E到x轴的距离为4，过点E作x轴的平行线a，与y轴交于点A．点P从点E处出发，以每秒2cm的速度沿直线a向左移动，点Q从原点O同时出发，以每秒1cm的速度沿x轴向右移动．
  ①经过几秒PQ平行于y轴？
  
  ②若某一时刻以A，O，Q，P为顶点的四边形的面积是10cm² ，求此时点P的坐标．
答案解析收藏纠错 + 选题
23. 勾股定理是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦。我国西汉《周髀算经》中周公与商高对话中涉及勾股定理，所以这个定理也有人称商高定理，勾股定理在西方被称为毕达哥拉斯定理，相传是古希腊数学家兼哲学家毕达哥拉斯于公元前550年发现的。
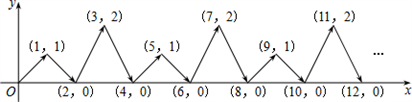
我们知道，可以用一个数表示数轴上的一个点，而每个数在数轴上也有一个点与之对应。现在把这个数轴叫做x轴，同时，增加一个垂直于x轴的数轴，叫做y轴，如下图。这样，我们可以用一组数对来表示平面上的一个点，同时，平面上的一个点也可以用一组数对来表示，比如下图中A点的位置可以表示为（2，3），而数对（2，3）所对应的点即为A。若平面上的点M $\text{[math]}$ ，N $\text{[math]}$ ，我们定义点M、N在x轴方向上的距离为： $\text{[math]}$ ，点M、N在y轴方向上的距离为： $\text{[math]}$ 。例如，点G（3，4）与点H（1，-1）在x轴方向上的距离为：|3-1|=2，点M、N在y轴方向上的距离为：|4-（-1）|=5。
1. （1）若点B位置为（-1，-1），请在图中画出点B；图中点C的位置用数对来表示。
2. （2）在（1）条件下，A、B两点在x轴方向上的距离为，在y轴方向上的距离为，A、B两点间的距离为；若E点、F点的位置分别为（a，b）、（c，d），点E、F之间的距离为|EF|，则 $\text{[math]}$ =。
3. （3）有一个点D，它与（0，0）点的距离为1，请画出D点所有可能的位置。
答案解析收藏纠错 + 选题