2017年四川省成都市高考数学二诊试卷（理科）

更新时间：2017-04-20 浏览次数：603 类型：高考模拟

一、选择题

1. 设集合A=[﹣1，2]，B={y|y=x² ， x∈A}，则A∩B=（）

A . [1，4] B . [1，2] C . [﹣1，0] D . [0，2]

答案解析收藏纠错 + 选题
2. 若复数z₁=a+i（a∈R），z₂=1﹣i，且 $\text{[math]}$ 为纯虚数，则z₁在复平面内所对应的点位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. 在等比数列{a_n}中，已知a₃=6，a₃+a₅+a₇=78，则a₅=（）

A . 12 B . 18 C . 24 D . 36

答案解析收藏纠错 + 选题
4. 已知平面向量 $\text{[math]}$ ， $\text{[math]}$ 的夹角为 $\text{[math]}$ ，且| $\text{[math]}$ |=1，| $\text{[math]}$ |= $\text{[math]}$ ，则 $\text{[math]}$ +2 $\text{[math]}$ 与 $\text{[math]}$ 的夹角是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. 若曲线y=lnx+ax²（a为常数）不存在斜率为负数的切线，则实数a的取值范围是（）

A . （﹣ $\text{[math]}$ ，+∞） B . [﹣ $\text{[math]}$ ，+∞） C . （0，+∞） D . [0，+∞）

答案解析收藏纠错 + 选题
6. 若实数x，y满足不等式 $\text{[math]}$ ，且x﹣y的最大值为5，则实数m的值为（）

A . 0 B . ﹣1 C . ﹣2 D . ﹣5

答案解析收藏纠错 + 选题
7. 已知m，n是空间中两条不同的直线，α、β是两个不同的平面，且m⊂α，n⊂β．有下列命题：

①若α∥β，则m∥n；
②若α∥β，则m∥β；
③若α∩β=l，且m⊥l，n⊥l，则α⊥β；
④若α∩β=l，且m⊥l，m⊥n，则α⊥β．
其中真命题的个数是（）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
8. 已知函数f（x）=a^x（a＞0，a≠1）的反函数的图象经过点（ $\text{[math]}$ ， $\text{[math]}$ ）．若函数g（x）的定义域为R，当x∈[﹣2，2]时，有g（x）=f（x），且函数g（x+2）为偶函数，则下列结论正确的是（）

A . g（π）＜g（3）＜g（ $\text{[math]}$ ） B . g（π）＜g（ $\text{[math]}$ ）＜g（3） C . g（ $\text{[math]}$ ）＜g（3）＜g（π） D . g（ $\text{[math]}$ ）＜g（π）＜g（3）

答案解析收藏纠错 + 选题
9. 执行如图所示的程序框图，若输入a，b，c分别为1，2，0.3，则输出的结果为（）

A . 1.125 B . 1.25 C . 1.3125 D . 1.375

答案解析收藏纠错 + 选题
10. 已知函数f（x）=sin（ωx+2φ）﹣2sinφcos（ωx+φ）（ω＞0，φ∈R）在（π， $\text{[math]}$ ）上单调递减，则ω的取值范围是（）

A . （0，2] B . （0， $\text{[math]}$ ] C . [ $\text{[math]}$ ，1] D . [ $\text{[math]}$ ， $\text{[math]}$ ]

答案解析收藏纠错 + 选题
11. 设双曲线C： $\text{[math]}$ （a＞0，b＞0）的左右焦点分别为F₁ ， F₂ ，以F₁F₂为直径的圆与双曲线左支的一个交点为P，若以OF₁（O为坐标原点）为直径的圆与PF₂相切，则双曲线C的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. 把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影．如图，在三棱锥A﹣BCD中，BD⊥CD，AB⊥DB，AC⊥DC，AB=DB=5，CD=4，将围成三棱锥的四个三角形的面积从小到大依次记为S₁ ， S₂ ， S₃ ， S₄ ，设面积为S₂的三角形所在的平面为α，则面积为S₄的三角形在平面α上的射影的面积是（）

A . 2 $\text{[math]}$ B . $\text{[math]}$ C . 10 D . 30

答案解析收藏纠错 + 选题

二、填空题

13. 在二项式（ax²+ $\text{[math]}$ ）⁵的展开式中，若常数项为﹣10，则a=．

答案解析收藏纠错 + 选题
14. 在一个容量为5的样本中，数据均为整数，已测出其平均数为10，但墨水污损了两个数据，其中一个数据的十位数字1未污损，即9，10，11，，那么这组数据的方差s²可能的最大值是．

答案解析收藏纠错 + 选题
15. (2017·银川模拟) 如图，抛物线y²=4x的一条弦AB经过焦点F，取线段OB的中点D，延长OA至点C，使|OA|=|AC|，过点C，D作y轴的垂线，垂足分别为E，G，则|EG|的最小值为．

答案解析收藏纠错 + 选题
16. 在数列{a_n}中，a₁=1，a_n= $\text{[math]}$ a_n_﹣₁（n≥2，n∈N^*），则数列{ $\text{[math]}$ }的前n项和T_n=．

答案解析收藏纠错 + 选题

三、解答题

17. 如图，在平面四边形ABCD中，已知∠A= $\text{[math]}$ ，∠B= $\text{[math]}$ ，AB=6，在AB边上取点E，使得BE=1，连接EC，ED．若∠CED= $\text{[math]}$ ，EC= $\text{[math]}$ ．
（Ⅰ）求sin∠BCE的值；
（Ⅱ）求CD的长．

答案解析收藏纠错 + 选题
18. 某项科研活动共进行了5次试验，其数据如表所示：
特征量
第1次
第2次
第3次
第4次
第5次
x
555
559
551
563
552
y
601
605
597
599
598
（Ⅰ）从5次特征量y的试验数据中随机地抽取两个数据，求至少有一个大于600的概率；
（Ⅱ）求特征量y关于x的线性回归方程 $\text{[math]}$ ；并预测当特征量x为570时特征量y的值．
（附：回归直线的斜率和截距的最小二乘法估计公式分别为 $\text{[math]}$ = $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
19. 如图，已知梯形CDEF与△ADE所在平面垂直，AD⊥DE，CD⊥DE，AB∥CD∥EF，AE=2DE=8，AB=3，EF=9．CD=12，连接BC，BF．
（Ⅰ）若G为AD边上一点，DG= $\text{[math]}$ DA，求证：EG∥平面BCF；
（Ⅱ）求二面角E﹣BF﹣C的余弦值．

答案解析收藏纠错 + 选题
20. 在平面直角坐标系xOy中，已知椭圆E： $\text{[math]}$ （a＞b＞0），圆O：x²+y²=r²（0＜r＜b），若圆O的一条切线l：y=kx+m与椭圆E相交于A，B两点．

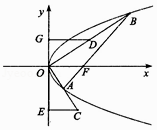
（Ⅰ）当k=﹣ $\text{[math]}$ ，r=1时，若点A，B都在坐标轴的正半轴上，求椭圆E的方程；
（Ⅱ）若以AB为直径的圆经过坐标原点O，探究a，b，r之间的等量关系，并说明理由．

答案解析收藏纠错 + 选题
21. 已知函数f（x）=alnx﹣x+ $\text{[math]}$ ，其中a＞0
（Ⅰ）若f（x）在（2，+∞）上存在极值点，求a的取值范围；
（Ⅱ）设x₁∈（0，1），x₂∈（1，+∞），若f（x₂）﹣f（x₁）存在最大值，记为M（a）．则a≤e+ $\text{[math]}$ 时，M（a）是否存在最大值？若存在，求出最大值；若不存在，请说明理由．

答案解析收藏纠错 + 选题
22. 选修4-4：坐标系与参数方程

在直角坐标系xOy中，曲线C的参数方程为 $\text{[math]}$ （α为参数），直线l的参数方程为 $\text{[math]}$ （t为参数），在以坐标原点O为极点，x轴为正半轴为极轴的极坐标系中，过极点O的射线与曲线C相交于不同于极点的点A，且点A的极坐标为（2 $\text{[math]}$ ，θ），其中θ∈（ $\text{[math]}$ ，π）
（Ⅰ）求θ的值；
（Ⅱ）若射线OA与直线l相交于点B，求|AB|的值．

答案解析收藏纠错 + 选题
23. 选修4-5：不等式选讲
已知函数f（x）=4﹣|x|﹣|x﹣3|
（Ⅰ）求不等式f（x+ $\text{[math]}$ ）≥0的解集；
（Ⅱ）若p，q，r为正实数，且 $\text{[math]}$ =4，求3p+2q+r的最小值．

答案解析收藏纠错 + 选题