云南省红河州蒙自市2018届数学中考模拟试卷（4月份）

更新时间：2019-05-09 浏览次数：383 类型：中考模拟

一、单选题

1. (2023八下·叙州期末) 某种病毒近似于球体，它的半径约为0.000000005米，用科学记数法表示为（）

A . 5×10⁸ B . 5×10⁹ C . 5×10^﹣8 D . 5×10^﹣9

答案解析收藏纠错 + 选题
2. (2019·海曙模拟) 如图，AB∥CD，那么（）

A . ∠BAD与∠B互补 B . ∠1=∠2 C . ∠BAD与∠D互补 D . ∠BCD与∠D互补

答案解析收藏纠错 + 选题
3. (2018·蒙自模拟) 下列运算或变形正确的是（）

A . ﹣2a+2b=﹣2（a+b） B . a²﹣2a+4=（a﹣2）² C . （2a²）³=6a⁶ D . 3a²•2a³=6a⁵

答案解析收藏纠错 + 选题
4. (2018·蒙自模拟) 反比例函数y= $\text{[math]}$ 的图象向右平移 $\text{[math]}$ 个单位长度得到一个新的函数，当自变量x取1，2，3，4，5，…，（正整数）时，新的函数值分别为y₁ ， y₂ ， y₃ ， y₄ ， y₅ ， …，其中最小值和最大值分别为（）

A . y₁ ， y₂ B . y₄₃ ， y₄₄ C . y₄₄ ， y₄₅ D . y₂₀₁₄ ， y₂₀₁₅

答案解析收藏纠错 + 选题
5. (2018·蒙自模拟) 有以下图形：平行四边形、矩形、等腰三角形、线段、菱形，其中既是轴对称图形又是中心对称图形的有（）

A . 5个 B . 4个 C . 3个 D . 2个

答案解析收藏纠错 + 选题

6. (2020·锦州模拟) 某校八年级两个班，各选派10名学生参加学校举行的“古诗词”大赛，各参赛选手成绩的数据分析如表所示，则以下判断错误的是（）

班级	平均数	中位数	众数	方差
八（1）班	94	93	94	12
八（2）班	95	95.5	93	8.4

A . 八（2）班的总分高于八（1）班 B . 八（2）班的成绩比八（1）班稳定 C . 两个班的最高分在八（2）班 D . 八（2）班的成绩集中在中上游

答案解析收藏纠错 + 选题

7. (2018·蒙自模拟) 已知⊙O的半径为10，P为⊙O内一点，且OP=6，则过P点，且长度为整数的弦有（）

A . 5条 B . 6条 C . 8条 D . 10条

答案解析收藏纠错 + 选题
8. (2018·蒙自模拟) 二维码已经给我们的生活带来了很大方便，它是由大小相同的黑白两色的小正方形（如图1中C）按某种规律组成的一个大正方形，现有25×25格式的正方形如图1，角上是三个7×7的A型大黑白相间正方形，中间右下一个5×5的B型黑白相间正方形，除这4个正方形外，若其他的小正方形白色块数y与黑色块数x正好满足如图2所示的函数图象，则该25×25格式的二维码共有多少块黑色的C型小正方形（）

A . 153 B . 218 C . 100 D . 216

答案解析收藏纠错 + 选题

二、填空题

9. (2018·蒙自模拟) 结合具体的数，通过特例进行归纳，判断“如果a大于b，那么a的倒数小于b的倒数”，这句话的对错，你给出的特例是：a=，b=．你认为（填“对”或“错”）．

答案解析收藏纠错 + 选题
10. (2018·蒙自模拟) 若不等式组 $\text{[math]}$ 的解集是x＜4，则m的取值范围是．

答案解析收藏纠错 + 选题
11. (2018·蒙自模拟) 如图，已知CO₁是△ABC的中线，过点O₁作O₁E₁∥AC交BC于点E₁ ，连接AE₁交CO₁于点O₂；过点O₂作O₂E₂∥AC交BC于点E₂ ，连接AE₂交CO₁于点O₃；过点O₃作O₃E₃∥AC交BC于点E₃ ， …，如此继续，可以依次得到点O₄ ， O₅ ， …，O_n和点E₄ ， E₅ ， …，E_n ，则O₂₀₁₆E₂₀₁₆=AC．

答案解析收藏纠错 + 选题
12. (2018·蒙自模拟) 已知函数 $\text{[math]}$ ，则x取值范围是．

答案解析收藏纠错 + 选题
13. (2018·蒙自模拟) 一个几何体的三视图如图，很据图示的数据计算该几何体的表面积为（结果保留π）．

答案解析收藏纠错 + 选题
14. (2018·蒙自模拟) 如图，函数y=kx+b的图象与x轴，y轴分别交于A（﹣2，0），B（0，1）两点，那么此函数的图象与函数y=x﹣1的图象交点C的坐标是．

答案解析收藏纠错 + 选题

三、解答题

15. (2018·蒙自模拟) 计算：（ $\text{[math]}$ ﹣2）⁰+ $\text{[math]}$ +4cos30°﹣|﹣ $\text{[math]}$ |．

答案解析收藏纠错 + 选题
16. (2023七下·砀山期末) 如图所示，一个四边形纸片ABCD，∠B=∠D=90°，把纸片按如图所示折叠，使点B落在AD边上的B′点，AE是折痕．
1. （1）试判断B′E与DC的位置关系；
2. （2）如果∠C=130°，求∠AEB的度数．
答案解析收藏纠错 + 选题
17. (2021七下·岱岳期中) 随着中国传统节日“端午节”的临近，东方红商场决定开展“欢度端午，回馈顾客”的让利促销活动，对部分品牌粽子进行打折销售，其中甲品牌粽子打八折，乙品牌粽子打七五折，已知打折前，买6盒甲品牌粽子和3盒乙品牌粽子需660元；打折后，买50盒甲品牌粽子和40盒乙品牌粽子需要5200元．
1. （1）打折前甲、乙两种品牌粽子每盒分别为多少元？
2. （2）阳光敬老院需购买甲品牌粽子80盒，乙品牌粽子100盒，问打折后购买这批粽子比不打折节省了多少钱？
答案解析收藏纠错 + 选题
18. (2018·蒙自模拟) 学习习近平总书记关于生态文明建设重要井话，牢固树立“绿水青山就是金山银山”的科学观，让环保理念深入到学校，某校张老师为了了解本班学生3月植树成活情况，对本班全体学生进行了调查，并将调查结果分为了三类：A好，B：中，C：差．

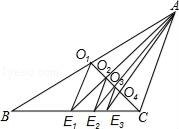
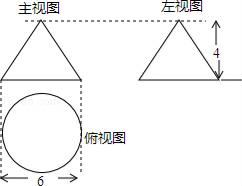
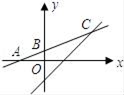
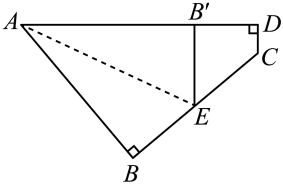
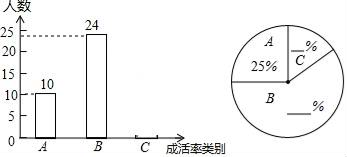
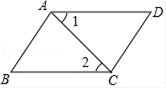
请根据图中信息，解答下列问题：
1. （1）求全班学生总人数；
2. （2）将上面的条形统计图与扇形统计图补充完整；
3. （3）张老师在班上随机抽取了4名学生，其中A类1人，B类2人，C类1人，若再从这4人中随加抽取2人，请用画对状图或列表法求出全是B类学生的概率．
答案解析收藏纠错 + 选题
19. (2018·蒙自模拟) 在矩形ABCD中，将点A翻折到对角线BD上的点M处，折痕BE交AD于点E．将点C翻折到对角线BD上的点N处，折痕DF交BC于点F．
1. （1）求证：四边形BFDE为平行四边形；
2. （2）若四边形BFDE为菱形，且AB=3，求BC的长．
答案解析收藏纠错 + 选题
20. (2018·蒙自模拟) 填空： $\text{[math]}$ =1﹣ $\text{[math]}$ ， $\text{[math]}$ = $\text{[math]}$ ﹣ $\text{[math]}$ ， $\text{[math]}$ = $\text{[math]}$ ﹣ $\text{[math]}$ ， $\text{[math]}$ = $\text{[math]}$ ﹣ $\text{[math]}$ ，…．
1. （1）试求 $\text{[math]}$ =， $\text{[math]}$ =．
2. （2）请猜想能表示上述规律的等式，并用含字母n（n 整数）的式子表示出来
3. （3）请你直接利用（2）所得的结论计算下列式子：
  $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2018·蒙自模拟) 如图，AB为⊙O的直径，CD切⊙O于点C，与BA的延长线交于点D，OE⊥AB交⊙O于点E，连接CA、CE、CB，CE交AB于点G，过点A作AF⊥CE于点F，延长AF交BC于点P．

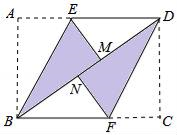
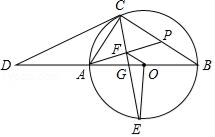
（Ⅰ）求∠CPA的度数；

（Ⅱ）连接OF，若AC= $\text{[math]}$ ，∠D=30°，求线段OF的长．

答案解析收藏纠错 + 选题
22. (2018·蒙自模拟) 如图1，在平面直角坐标系xOy中，直线l： $\text{[math]}$ 与x轴、y轴分别交于点A和点B（0，﹣1），抛物线 $\text{[math]}$ 经过点B，且与直线l的另一个交点为C（4，n）．
1. （1）求n的值和抛物线的解析式；
2. （2）点D在抛物线上，且点D的横坐标为t（0＜t＜4）．DE∥y轴交直线l于点E，点F在直线l上，且四边形DFEG为矩形（如图2）．若矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值；
3. （3） M是平面内一点，将△AOB绕点M沿逆时针方向旋转90°后，得到△A₁O₁B₁ ，点A、O、B的对应点分别是点A₁、O₁、B₁ ．若△A₁O₁B₁的两个顶点恰好落在抛物线上，请直接写出点A₁的横坐标．
答案解析收藏纠错 + 选题