2014年浙江省宁波市中考数学试卷

更新时间：2017-04-25 浏览次数：1063 类型：中考真卷

一、选择题

1. (2014·宁波) 下列各数中，既不是正数也不是负数的是（）

A . 0 B . ﹣1 C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
2. (2014·宁波) 宁波轨道交通1号线、2号线建设总投资253.7亿元，其中253.7亿用科学记数法表示为（）

A . 253.7×10⁸ B . 25.37×10⁹ C . 2.537×10¹⁰ D . 2.537×10¹¹

答案解析收藏纠错 + 选题
3. (2022七上·昌黎期中) 用矩形纸片折出直角的平分线，下列折法正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023七上·江油期中) 杨梅开始采摘啦！每筐杨梅以5千克为基准，超过的千克数记为正数，不足的千克数记为负数，记录如图，则这4筐杨梅的总质量是（）

A . 19.7千克 B . 19.9千克 C . 20.1千克 D . 20.3千克

答案解析收藏纠错 + 选题
5. (2014·宁波) 圆锥的母线长为4，底面半径为2，则此圆锥的侧面积是（）

A . 6π B . 8π C . 12π D . 16π

答案解析收藏纠错 + 选题
6. (2024八下·哈尔滨期中) 菱形的两条对角线长分别是6和8，则此菱形的边长是（）

A . 10 B . 8 C . 6 D . 5

答案解析收藏纠错 + 选题
7. (2020九上·吴兴期中) 如图，在2×2的正方形网格中有9个格点，已经取定点A和B，在余下的7个点中任取一点C，使△ABC为直角三角形的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2014·宁波) 如图，梯形ABCD中，AD∥BC，∠B=∠ACD=90°，AB=2，DC=3，则△ABC与△DCA的面积比为（）

A . 2：3 B . 2：5 C . 4：9 D . $\text{[math]}$ ： $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2014·宁波) 已知命题“关于x的一元二次方程x²+bx+1=0，当b＜0时必有实数解”，能说明这个命题是假命题的一个反例可以是（）

A . b=﹣1 B . b=2 C . b=﹣2 D . b=0

答案解析收藏纠错 + 选题
10. (2014·宁波) 如果一个多面体的一个面是多边形，其余各面是有一个公共顶点的三角形，那么这个多面体叫做棱锥．如图是一个四棱柱和一个六棱锥，它们各有12条棱．下列棱柱中和九棱锥的棱数相等的是（）

A . 五棱柱 B . 六棱柱 C . 七棱柱 D . 八棱柱

答案解析收藏纠错 + 选题
11. (2023九上·西安开学考) 如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是（）

A . 2.5 B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
12. (2014·宁波) 已知点A（a﹣2b，2﹣4ab）在抛物线y=x²+4x+10上，则点A关于抛物线对称轴的对称点坐标为（）

A . （﹣3，7） B . （﹣1，7） C . （﹣4，10） D . （0，10）

答案解析收藏纠错 + 选题

二、填空题

13. (2014·宁波) ﹣4的绝对值是．

答案解析收藏纠错 + 选题
14. (2014·宁波) 方程 $\text{[math]}$ = $\text{[math]}$ 的根x=．

答案解析收藏纠错 + 选题
15. (2014·宁波) 某冷饮店一天售出各种口味雪糕数量的扇形统计图如图，其中售出红豆口味的雪糕200支，那么售出水果口味雪糕的数量是支．

答案解析收藏纠错 + 选题
16. (2014·宁波) 一个大正方形和四个全等的小正方形按图①、②两种方式摆放，则图②的大正方形中未被小正方形覆盖部分的面积是（用a、b的代数式表示）．

答案解析收藏纠错 + 选题
17. (2014·宁波)
为解决停车难的问题，在如图一段长56米的路段开辟停车位，每个车位是长5米宽2.2米的矩形，矩形的边与路的边缘成45°角，那么这个路段最多可以划出个这样的停车位．（ $\text{[math]}$ ≈1.4）

答案解析收藏纠错 + 选题
18. (2014·宁波) 如图，半径为6cm的⊙O中，C、D为直径AB的三等分点，点E、F分别在AB两侧的半圆上，∠BCE=∠BDF=60°，连接AE、BF，则图中两个阴影部分的面积为 cm² ．

答案解析收藏纠错 + 选题

三、解答题

19. (2014·宁波) 计算下列各题.
1. （1）化简：（a+b）²+（a﹣b）（a+b）﹣2ab；
2. （2）解不等式：5（x﹣2）﹣2（x+1）＞3．
答案解析收藏纠错 + 选题
20. (2014·宁波) 作为宁波市政府民生实事之一的公共自行车建设工作已基本完成，某部门对今年4月份中的7天进行了公共自行车日租车量的统计，结果如图：
1. （1）求这7天日租车量的众数、中位数和平均数；
2. （2）用（1）中的平均数估计4月份（30天）共租车多少万车次；
3. （3）市政府在公共自行车建设项目中共投入9600万元，估计2014年共租车3200万车次，每车次平均收入租车费0.1元，求2014年租车费收入占总投入的百分率（精确到0.1%）．
答案解析收藏纠错 + 选题
21. (2014·宁波) 如图，从A地到B地的公路需经过C地，图中AC=10千米，∠CAB=25°，∠CBA=37°，因城市规划的需要，将在A、B两地之间修建一条笔直的公路．
1. （1）求改直的公路AB的长；
2. （2）问公路改直后比原来缩短了多少千米？（sin25°≈0.42，cos25°≈0.91，sin37°≈0.60，tan37°≈0.75）
答案解析收藏纠错 + 选题
22. (2014·宁波)
如图，点A、B分别在x，y轴上，点D在第一象限内，DC⊥x轴于点C，AO=CD=2，AB=DA= $\text{[math]}$ ，反比例函数y= $\text{[math]}$ （k＞0）的图象过CD的中点E．
1. （1）求证：△AOB≌△DCA；
2. （2）求k的值；
3. （3） △BFG和△DCA关于某点成中心对称，其中点F在y轴上，是判断点G是否在反比例函数的图象上，并说明理由．
答案解析收藏纠错 + 选题
23. (2014·宁波) 如图，已知二次函数y=ax²+bx+c的图象过A（2，0），B（0，﹣1）和C（4，5）三点．
1. （1）求二次函数的解析式；
2. （2）设二次函数的图象与x轴的另一个交点为D，求点D的坐标；
3. （3）在同一坐标系中画出直线y=x+1，并写出当x在什么范围内时，一次函数的值大于二次函数的值．
答案解析收藏纠错 + 选题
24. (2014·宁波) 用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成，硬纸板以如图两种方法裁剪（裁剪后边角料不再利用）．
A方法：剪6个侧面； B方法：剪4个侧面和5个底面．
现有19张硬纸板，裁剪时x张用A方法，其余用B方法．
1. （1）用x的代数式分别表示裁剪出的侧面和底面的个数；
2. （2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？
答案解析收藏纠错 + 选题
25. (2014·宁波) 课本的作业题中有这样一道题：把一张顶角为36°的等腰三角形纸片剪两刀，分成3张小纸片，使每张小纸片都是等腰三角形，你能办到吗？请画示意图说明剪法．
我们有多少种剪法，图1是其中的一种方法：
定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段叫做这个三角形的三分线．
1. （1）请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数；（若两种方法分得的三角形成3对全等三角形，则视为同一种）
2. （2） △ABC中，∠B=30°，AD和DE是△ABC的三分线，点D在BC边上，点E在AC边上，且AD=BD，DE=CE，设∠C=x°，试画出示意图，并求出x所有可能的值；
3. （3）如图3，△ABC中，AC=2，BC=3，∠C=2∠B，请画出△ABC的三分线，并求出三分线的长．
答案解析收藏纠错 + 选题
26. (2014·宁波)
木匠黄师傅用长AB=3，宽BC=2的矩形木板做一个尽可能大的圆形桌面，他设计了四种方案：

方案一：直接锯一个半径最大的圆；
方案二：圆心O₁、O₂分别在CD、AB上，半径分别是O₁C、O₂A，锯两个外切的半圆拼成一个圆；
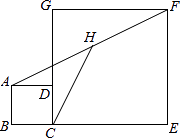
方案三：沿对角线AC将矩形锯成两个三角形，适当平移三角形并锯一个最大的圆；
方案四：锯一块小矩形BCEF拼到矩形AFED下面，利用拼成的木板锯一个尽可能大的圆．
1. （1）写出方案一中圆的半径；
2. （2）通过计算说明方案二和方案三中，哪个圆的半径较大？
3. （3）在方案四中，设CE=x（0＜x＜1），圆的半径为y．
  ①求y关于x的函数解析式；
  ②当x取何值时圆的半径最大，最大半径为多少？并说明四种方案中哪一个圆形桌面的半径最大．
答案解析收藏纠错 + 选题