河北省保定市安国市2018-2019学年八年级上学期数学期中...

更新时间：2019-04-03 浏览次数：588 类型：期中考试

一、选择题

1. (2019八上·安国期中) $\text{[math]}$ 的立方根是（）

A . 4 B . 2 C . $\text{[math]}$ D . 8

答案解析收藏纠错 + 选题
2. (2019八上·安国期中) 点P（-5，3）关于y轴的对称点的坐标是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2019八上·安国期中) 下列长度的三条线段不能组成直角三角形的是（）

A . 1，， $\text{[math]}$ B . $\text{[math]}$ ，， $\text{[math]}$ C . 5，4，3 D . ，2，

答案解析收藏纠错 + 选题
4. (2019八上·安国期中) 如图，点A（-1，2），则点B的坐标为（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2019八上·安国期中) 下列二次根式中是最简二次根式的是（）

A . $\text{[math]}$ B . C . D .

答案解析收藏纠错 + 选题
6. (2019八上·安国期中) 下列运算正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2019八上·安国期中) 设 $\text{[math]}$ 的小数部分为b，则b（b+3）的值是（）

A . 1 B . C . 3 D . 无法确定

答案解析收藏纠错 + 选题
8. (2020九上·丰县月考) 在平面直角坐标系中，过点（1，2）作直线l，若直线l与两坐标轴围成的三角形面积为4，则满足条件的直线l的条数是（）。

A . 5 B . 4 C . 3 D . 2

答案解析收藏纠错 + 选题
9. (2019八上·安国期中) 一次函数y=kx-1的图象经过点P，且y的值随x值的增大而增大，则点P的坐标可以为（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2019八上·安国期中) 如图，直线l是一次函数y=kx+b的图象，若点A（3，m）在直线l上，则m的值是（）

A . B . $\text{[math]}$ C . D . 7

答案解析收藏纠错 + 选题
11. (2019八上·安国期中) 如图，已知一个直角三角板的直角顶点与原点重合，另两个顶点A，B的坐标分别为（-1，0），（0， $\text{[math]}$ ）．现将该三角板向右平移使点A与点O重合，得到△OCB′，则点B的对应点B′的坐标是（）

A . B . C . D .

答案解析收藏纠错 + 选题
12. (2019八上·安国期中) 如图，利用三个面积分别为5，x，y的正方形拼成一个直角三角形，则y关于x之间的函数图象不经过（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
13. (2019八上·安国期中) 把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个锐角顶点与另一个的直角顶点重合于点A，且另外三个锐角顶点B，C，D在同一条直线上，若AB= $\text{[math]}$ ，则CD的长为（）

A . B . C . D . $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2019八上·安国期中) 如图：三个正比例函数的图象分别对应的解析式是①y=ax，②y=bx，③y=cx，则a、b、c的大小关系是（）

A . B . C . D .

答案解析收藏纠错 + 选题
15. (2019八上·安国期中) 如图中表示一次函数y=mx+n与正比例函数y=mnx（m、n是常数，mn≠0）图象的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
16. (2019八上·安国期中) 如图，在平面直角坐标系中，点M是直线y=-x上的点，过点M作MN⊥x轴，交直线y=x于点N，当MN≤8时，设点M的横坐标为m，则m的取值范围为（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

17. (2019八上·安国期中) 若点A（a+1，b-2）在第二象限，则点B（-a，1-b）在第象限．

答案解析收藏纠错 + 选题
18. (2019八上·安国期中) 如图，圆柱形玻璃杯高为13cm，底面周长为40cm，在杯内壁离底1cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿3cm与蜂蜜相对的点A处，则蚂蚁从外壁到内壁B处的最短距离为．

答案解析收藏纠错 + 选题
19. (2019八上·安国期中) 汽车行驶前，油箱中有油55L，已知每百千米汽车耗油10L，油箱中的余油量Q（L）与它行驶的距离s（百千米）之间的函数关系式为，为了保证行车安全，油箱中至少存油5L．则汽车最多可行驶km．

答案解析收藏纠错 + 选题

三、计算题

20. (2019八上·安国期中) 计算下列各题
1. （1） $\text{[math]}$ ×（ $\text{[math]}$ -1）
2. （2） 2× $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2019八上·安国期中) 某游泳馆每年夏季推出两种游泳付费方式，方式一：先购买会员证，每张会员证100元，只限本人当年使用，凭证游泳每次再付费5元；方式二：不购买会员证，每次游泳付费9元．
1. （1）分别写出两种方式所花费用y（元）与游泳次数x（次）之间的函数关系式；
2. （2）若洋洋今年夏季游泳的总费用为270元，选择哪种付费方式，他游泳的次数比较多？
3. （3）游泳多少次时，洋洋选择两种方式付费相同？
4. （4）优优说今年夏季我最多游泳20次，他选择哪种方式更合算？并说明理由．
答案解析收藏纠错 + 选题

四、解答题

22. (2019八上·安国期中) 如图是某个海岛的平面示意图，如果哨所1的坐标是（1，3），哨所2的坐标是（-2，0），请你先建立平面直角坐标系，并用坐标表示出小广场、雷达、营房、码头的位置．

答案解析收藏纠错 + 选题
23. (2019八上·安国期中) 已知y-4与x成正比，当x=1时，y=2
1. （1）求y与x之间的函数关系式，在下列坐标系中画出函数图象；
2. （2）当x= $\text{[math]}$ 时，求函数y的值；
3. （3）结合图象和函数的增减性，求当y＜-2时自变量x的取值范围．
答案解析收藏纠错 + 选题

24. (2019八上·安国期中) 嘉嘉参加机器人设计活动，需操控机器人在5×5的方格棋盘上从A点行走至B点，且每个小方格皆为正方形，主办单位规定了三条行走路径R₁ ， R₂ ， R₃ ，其行经位置如图与表所示：

路径	编号	图例	行径位置
第一条路径	R₁		A→C→D→B
第二条路径	R₂		A→E→D→F→B
第三条路径	R₃		A→G→B

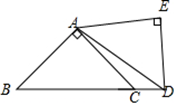
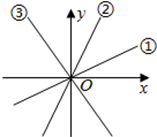
已知A、B、C、D、E、F、G七点皆落在格线的交点上，且两点之间的路径皆为直线，在无法使用任何工具测量的条件下，请判断R₁、R₂、R₃这三条路径中，最长与最短的路径分别为何？请写出你的答案，并完整说明理由．

答案解析收藏纠错 + 选题

25. (2019八上·安国期中) 观察下列各式及验证过程
$\text{[math]}$ = $\text{[math]}$ ，验证： $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ；

$\text{[math]}$ = $\text{[math]}$ ，验证： $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ；

$\text{[math]}$ = $\text{[math]}$ ，验证： $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ；
1. （1）按照上述三个等式及其验证过程的基本思路，猜想 $\text{[math]}$ =；
2. （2）按照上述三个等式及其验证过程的基本思路，猜想 $\text{[math]}$ 的变形结果并进行验证；
3. （3）针对上述各式反映的规律，写出用n（n≥2的自然数）表示的等式，并进行验证．
答案解析收藏纠错 + 选题
26. (2019八上·安国期中) 在平面几何中，我们学过两条直线平行的定义，下面就两个一次函数的图象所确定的两条直线，给出它们平行的定义：设一次函数y=k₁x+b₁（k₁≠0）的图象为直线l₁ ，一次函数y=k₂x+b₂（k₂≠0）的图象为直线l₂ ，若k₁=k₂ ，且b₁≠b₂ ，我们就称直线l₁与直线l₂互相平行．解答下面的问题：
1. （1）求过点P（1，2），且与已知直线y=-2x-1平行的直线l的函数解析式，并画出图象；
2. （2）设直线l分别与y轴，x轴交于点A、B，如果直线m：y=kx+t（t＞0）与直线l平行，且交x轴于点C，求出△ABC的面积S关于t函数关系式．
答案解析收藏纠错 + 选题