2019年高中物理高考二轮复习专题15：碰撞与动量守恒

如图所示是质量为M=1.5kg的小球A和质量为m=0.5kg的小球B在光滑水平面上做对心碰撞前后画出的位移x﹣时间t图象，由图可知（   ）

如图所示，轻弹簧的一端固定在竖直墙上，光滑弧形槽固定在光滑的水平面上，弧形槽底端与水平面相切，一个质量为m的小物块从槽高h处开始自由下滑，下列说法正确的是（   ）

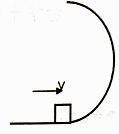
如图所示，将质量为M₁、半径为R且内壁光滑的半圆槽置于光滑水平面上，左侧靠墙角，右侧靠一质量为M₂的物块．今让一质量为m的小球自左侧槽口A的正上方h高处从静止开始落下，与圆弧槽相切自A点进入槽内，则以下结论中正确的是（   ）

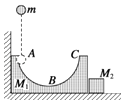
如图1所示，用“碰撞实验器“可以验证动量守恒定律，即研究两个小球在轨道水平部分碰撞前后的动量关系：

先安装好实验装置，在地上铺一张白纸，白纸上铺放复写纸，记下重垂线所指的位置O．

接下来的实验步骤如下：

步骤1：不放小球2，让小球1从斜槽上A点由静止滚下，并落在地面上．重复多次，用尽可能小的圆，把小球的所有落点圈在里面，其圆心就是小球落点的平均位置；

步骤2：把小球2放在斜槽前端边缘位置B，让小球1从A点由静止滚下，使它们碰撞．重复多次，并使用与步骤1同样的方法分别标出碰撞后两小球落点的平均位置；

步骤3：用刻度尺分别测量三个落地点的平均位置M、P、N离O点的距离，即线段OM、OP、ON的长度．

①对于上述实验操作，下列说法正确的是

A．应使小球每次从斜槽上相同的位置自由滚下

B．斜槽轨道必须光滑

C．斜槽轨道末端必须水平

D．小球1质量应大于小球2的质量

②上述实验除需测量线段OM、OP、ON的长度外，还需要测量的物理量有．

A．A、B两点间的高度差h₁

B．B点离地面的高度h₂

C．小球1和小球2的质量m₁、m₂

D．小球1和小球2的半径r

③当所测物理量满足表达式（用所测物理量的字母表示）时，即说明两球碰撞遵守动量守恒定律．如果还满足表达式（用所测物理量的字母表示）时，即说明两球碰撞时无机械能损失．

④完成上述实验后，某实验小组对上述装置进行了改造，如图2所示．在水平槽末端与水平地面间放置了一个斜面，斜面的顶点与水平槽等高且无缝连接．使小球1仍从斜槽上A点由静止滚下，重复实验步骤1和2的操作，得到两球落在斜面上的平均落点M′、P′、N′．用刻度尺测量斜面顶点到M′、P′、N′三点的距离分别为l₁、l₂、l₃ ． 则验证两球碰撞过程中动量守恒的表达式为（用所测物理量的字母表示）．

如图所示，质量为3m的木块静止放置在光滑水平面上，质量为m的子弹（可视为质点）以初速度v₀水平向右射入木块，穿出木块时速度变为 v₀ ， 已知木块的长为L，设子弹在木块中的阻力恒定．试求：

如图甲所示，ABC为水平轨道，与固定在竖直平面内的半圆形光滑轨道CD平滑连接，CD为竖直直径，轨道半径为R=0.2m．有一轻弹簧，左端固定在A点，弹簧处于自然状态时其右端恰好位于B点，B点左侧轨道AB光滑，右侧轨道BC动摩擦因数μ=0.1，BC长为L=1.0m；用质量为m=0.2kg的小物块缓慢压缩弹簧（不拴接），使弹簧储存一定弹性势能E_P后释放，物块经过B点继续运动从C点进入圆轨道，并通过D点；用力传感器测出小物块经过D点时对轨道压力F；改变弹簧压缩量，探究轨道D点受到压力F与弹簧弹性势能E_P的关系．弹簧形变都在弹性限度之内，重力加速度g取10m/s² ， 求：