广东省雷州市2018-2019学年高三上学期理数期末考试试卷

更新时间：2019-04-29 浏览次数：306 类型：期末考试

一、单选题

1. (2019高三上·雷州期末) 设集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·山东模拟) 若 $\text{[math]}$ （其中 $\text{[math]}$ 是虚数单位），则复数 $\text{[math]}$ 的共轭复数在复平面内对应的点位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. (2019高三上·雷州期末) 命题 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 为（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2019高三上·雷州期末) 已知双曲线C： $\text{[math]}$ 的离心率为 $\text{[math]}$ ，则C的渐近线方程为（）

A . y= $\text{[math]}$ B . y= $\text{[math]}$ C . y= $\text{[math]}$ D . y= $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2019高三上·雷州期末) 已知数列 $\text{[math]}$ 满足 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2019高三上·雷州期末) 赵爽是我国古代数学家、天文学家，大约在公元 $\text{[math]}$ 年，赵爽为《周髀算经》一书作序时，介绍了“勾股圆方图”，亦称“赵爽弦图”（以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的）．类比“赵爽弦图”，可类似地构造如图所示的图形，它是由 $\text{[math]}$ 个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形，设 $\text{[math]}$ ，若在大等边三角形内部（含边界）随机取一点，则此点取自小等边三角形（阴影部分）的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2019高三上·雷州期末) 已知 $\text{[math]}$ 是正方形 $\text{[math]}$ 的中心．若 $\text{[math]}$ ，其中 $\text{[math]}$ 、 $\text{[math]}$ $\text{[math]}$ ，则 $\text{[math]}$ ( ）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2019高三上·雷州期末) 函数 $\text{[math]}$ 的图像可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2019高三上·雷州期末) 点 $\text{[math]}$ 是抛物线 $\text{[math]}$ （ $\text{[math]}$ ）上的一点，点 $\text{[math]}$ 是焦点，则以线段 $\text{[math]}$ 为直径的圆与 $\text{[math]}$ 轴位置关系是（）

A . 相交 B . 相切 C . 相离 D . 以上三种均有可能

答案解析收藏纠错 + 选题
10. (2019高三上·雷州期末) 已知 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2019高三上·雷州期末) 正四面体 $\text{[math]}$ 中， $\text{[math]}$ 在平面 $\text{[math]}$ 内，点 $\text{[math]}$ 是线段 $\text{[math]}$ 的中点，在该四面体绕 $\text{[math]}$ 旋转的过程中，直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角不可能是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2019高三上·雷州期末) 已知函数 $\text{[math]}$ ， $\text{[math]}$ ，其中 $\text{[math]}$ 为自然对数的底数，若存在 $\text{[math]}$ 使 $\text{[math]}$ 成立，则实数 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2019高三上·雷州期末) 以下茎叶图记录了甲、乙两组各五名老师在一次学法（宪法部分）测试中的成绩（单位：分）

已知甲组数据的中位数是 $\text{[math]}$ ，乙组数据的平均数是 $\text{[math]}$ ，则 $\text{[math]}$ 的值等于．

答案解析收藏纠错 + 选题
14. (2019高三上·雷州期末) 若 $\text{[math]}$ ， $\text{[math]}$ 满足约束条件 $\text{[math]}$ ，则目标函数 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题
15. (2019高三上·雷州期末) 当 $\text{[math]}$ 时，函数 $\text{[math]}$ 取得最大值，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2019高三上·雷州期末) 某几何体的三视图如图所示，则该几何体的外接球的表面积为．

答案解析收藏纠错 + 选题

三、解答题

17. (2019高三上·雷州期末) 已知正项数列 $\text{[math]}$ 满足 $\text{[math]}$ ，且对任意 $\text{[math]}$ ， $\text{[math]}$ ．
（I）求数列 $\text{[math]}$ 的通项公式；

（II）设 $\text{[math]}$ ，求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2019高三上·雷州期末) 如图，三棱柱 $\text{[math]}$ 的所有棱长都是 $\text{[math]}$ ， $\text{[math]}$ 平面 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点．

（I）证明： $\text{[math]}$ $\text{[math]}$ 平面 $\text{[math]}$ ；

（II）求二面角 $\text{[math]}$ 的余弦值．

答案解析收藏纠错 + 选题
19. (2019高三上·雷州期末) 甲、乙两家销售公司拟各招聘一名产品推销员，日工资方案如下：甲公司规定底薪 $\text{[math]}$ 元，每销售一件产品提成 $\text{[math]}$ 元；乙公司规定底薪 $\text{[math]}$ 元，日销售量不超过 $\text{[math]}$ 件没有提成，超过 $\text{[math]}$ 件的部分每件提成 $\text{[math]}$ 元．
（I）请将两家公司各一名推销员的日工资 $\text{[math]}$ （单位：元）分别表示为日销售件数 $\text{[math]}$ 的函数关系式；

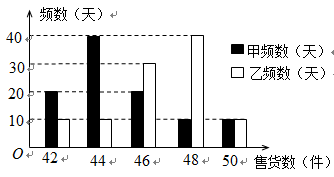
（II）从两家公司各随机选取一名推销员，对他们过去 $\text{[math]}$ 天的销售情况进行统计，得到如下条形图．若记甲公司该推销员的日工资为 $\text{[math]}$ ，乙公司该推销员的日工资为 $\text{[math]}$ （单位：元），将该频率视为概率，请回答下面问题：

某大学毕业生拟到两家公司中的一家应聘推销员工作，如果仅从日均收入的角度考虑，请你利用所学的统计学知识为他作出选择，并说明理由．

答案解析收藏纠错 + 选题
20. (2019高三上·雷州期末) 设 $\text{[math]}$ 、 $\text{[math]}$ 分别是椭圆 $\text{[math]}$ ： $\text{[math]}$ 的左、右焦点，若 $\text{[math]}$ 是该椭圆上的一个动点， $\text{[math]}$ 的最大值为 $\text{[math]}$ ．
（I）求椭圆 $\text{[math]}$ 的方程；

（II）设直线 $\text{[math]}$ 与椭圆 $\text{[math]}$ 交于 $\text{[math]}$ 、 $\text{[math]}$ 两点，点 $\text{[math]}$ 关于 $\text{[math]}$ 轴的对称点为 $\text{[math]}$ （ $\text{[math]}$ 与 $\text{[math]}$ 不重合)，试判定：直线 $\text{[math]}$ 与 $\text{[math]}$ 轴是否交于定点？若是，请写出定点坐标，并证明你的结论；否则，请说明理由．

答案解析收藏纠错 + 选题
21. (2019高三上·雷州期末) 已知函数 $\text{[math]}$ （ $\text{[math]}$ ）．
（I）求函数 $\text{[math]}$ 的单调区间；

（II）若存在 $\text{[math]}$ ，使 $\text{[math]}$ 成立，求整数 $\text{[math]}$ 的最小值．

答案解析收藏纠错 + 选题
22. (2019高三上·雷州期末) 在平面直角坐标系 $\text{[math]}$ 中，圆 $\text{[math]}$ 的参数方程为 $\text{[math]}$ ，( $\text{[math]}$ 为参数)，以坐标原点 $\text{[math]}$ 为极点， $\text{[math]}$ 轴正半轴为极轴建立极坐标系，圆 $\text{[math]}$ 的极坐标方程为 $\text{[math]}$
（Ⅰ）求圆 $\text{[math]}$ 的普通方程和圆 $\text{[math]}$ 的直角坐标方程；

（Ⅱ）判断圆 $\text{[math]}$ 与圆 $\text{[math]}$ 的位置关系．

答案解析收藏纠错 + 选题
23. (2019高三上·雷州期末) 已知函数 $\text{[math]}$ ．
（Ⅰ）求不等式 $\text{[math]}$ 的解集；

（Ⅱ）若关于x的方程 $\text{[math]}$ 存在实数解，求实数 $\text{[math]}$ 的取值范围．

答案解析收藏纠错 + 选题