一、选择题:本大题共10小题,每小题4分,满分40分
-
A . {1,2}
B . {2,7}
C . {1,7}
D . {1,2,7}
-
A . 球
B . 圆锥
C . 圆台
D . 圆柱
-
A . 0
B . 1
C . 10
D . (10,0)
-
A . (-∞,3)U(5,+∞)
B . (-∞,-8)U(-5,+∞)
C . (3,5)
D . (-5,-3)
-
A . (4,2)
B . (0,2)
C . (4,-2)
D . (-4.2)
-
6.
(2019·新宁模拟)
某校共有30个班,每个班的同学从1至45排学号,为了抽查学生体质达标情况,要求每班学号为9的同学进行交流体质检测,这里运用的抽样方法是( )
A . 系统抽样
B . 分层抽样
C . 抽签抽样
D . 随机抽样
-
-
8.
(2019·新宁模拟)
已知a=log
30.2,b=3
0.2 , c=0.2
3 , 则a,b,c三者的大小关系是( )
A . c>b>a
B . b>a>c
C . a>b>c
D . b>c>a
-
-
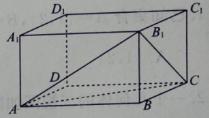
10.
(2019·新宁模拟)
如图长方体ABCD-A
1B
1C
1D
1中,底面ABCD是边长为2的正方形,棱BB
1长为

,连接BD交AC于O,连接B
1O,则B
1O与底面ABC所成角的大小是( )
二、填空题:本大题共5小题,每小题4分,满分20分。
-
-
-
-
-
15.
(2019·新宁模拟)
设m、几是两条不同的直线,α、β是两个不同的平面,给出下列四个命题:①若m∥αa,n∥a,则m∥n;②若m∥α,m∥β,则α∥β;③若m∥m,m⊥a,则n⊥a;@若m∥α,α⊥β,则m⊥β.其中正确的命题是
.
三、解答题,本大题共5小题,满分40分,解答应写出文字说明、证明过程或清算步骤
-
-
17.
(2019·新宁模拟)
已知数列{a
n}中,a
2=3,a
5=9,且点P(n,a
n)在一次函数y=kx+b的图象上.
-
(1)
求数列{an}的通项公式并证明(an}为等差数列;
-
(2)
记b
n=

,求数列{b
n}的前n和S
n.
-
-
-
(2)
判断函数y=f(x)的奇偶性,并说明理由;
-
-
19.
(2019·新宁模拟)
随机抽取某农场甲、乙两块树苗试验田各10棵油茶苗,测量他们的株高(单位:cm),获得株高数据的茎叶图如图所示.

-
-
(2)
现从乙中这10棵油茶苗中随机抽取2棵株高不低于176cm的油茶苗,求株高178cm的油茶苗被抽中的概率。
-
20.
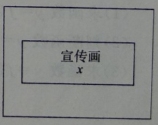
(2019·新宁模拟)
某广告公司计划利用一块临街建筑物墙面设计广告宣传画,宣传画是面积为32平方米的矩形,同时要求宣传画周围要留出前后宽2米,左右宽1米的空白区域(如图),设矩形宣传画的长为x米。
-
-
(2)
试问当x为多少时,矩形宣传画及周围空白区域的总面积y有最小值,最小值为多少?


