2014年江苏省淮安市中考数学试卷

更新时间：2024-07-12 浏览次数：524 类型：中考真卷

一、选择题

1. (2014·淮安) ﹣5的相反数为（）

A . ﹣ $\text{[math]}$ B . 5 C . $\text{[math]}$ D . ﹣5

答案解析收藏纠错 + 选题
2. (2014·淮安) 计算﹣a²+3a²的结果为（）

A . 2a² B . ﹣2a² C . 4a² D . ﹣4a²

答案解析收藏纠错 + 选题
3. (2014·淮安) 地球与月球的平均距离大约为384000km，将384000用科学记数法表示应为（）

A . 0.384×10⁶ B . 3.84×10⁶ C . 3.84×10⁵ D . 384×10³

答案解析收藏纠错 + 选题
4. (2014·淮安) 小华同学某体育项目7次测试成绩如下（单位：分）：9，7，10，8，10，9，10．这组数据的中位数和众数分别为（）

A . 8，10 B . 10，9 C . 8，9 D . 9，10

答案解析收藏纠错 + 选题
5. (2020九下·醴陵开学考) 如图，在边长为1个单位长度的小正方形组成的网格中，点A、B都是格点，则线段AB的长度为（）

A . 5 B . 6 C . 7 D . 25

答案解析收藏纠错 + 选题
6. (2014·淮安) 若式子 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是（）

A . x＜2 B . x＞2 C . x≤2 D . x≥2

答案解析收藏纠错 + 选题
7. (2014·淮安) 如图，直角三角板的直角顶点落在直尺边上，若∠1=56°，则∠2的度数为（）

A . 56° B . 44° C . 34° D . 28°

答案解析收藏纠错 + 选题
8. (2014·淮安) 如图，圆锥的母线长为2，底面圆的周长为3，则该圆锥的侧面积为（）

A . 3π B . 3 C . 6π D . 6

答案解析收藏纠错 + 选题

二、填空题

9. (2014·淮安) 因式分解：x²﹣3x=．

答案解析收藏纠错 + 选题
10. (2024九下·长沙模拟) 不等式组 $\text{[math]}$ 的解集为．

答案解析收藏纠错 + 选题
11. (2014·淮安) 若一个三角形三边长分别为2，3，x，则x的值可以为（只需填一个整数）

答案解析收藏纠错 + 选题
12. (2014·淮安) 一只不透明的袋子中装有1个白球和3个红球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，则摸出红球的概率为．

答案解析收藏纠错 + 选题
13. (2014·淮安) 如图，在四边形ABCD中，AB∥CD，要使得四边形ABCD是平行四边形，应添加的条件是（只填写一个条件，不使用图形以外的字母和线段）．

答案解析收藏纠错 + 选题
14. (2024七上·朝天期末) 若m²﹣2m﹣1=0，则代数式2m²﹣4m+3的值为．

答案解析收藏纠错 + 选题
15. (2019七下·河东期末) 如图，M、N、P、Q是数轴上的四个点，这四个点中最适合表示 $\text{[math]}$ 的点是．

答案解析收藏纠错 + 选题
16. (2020八上·徐州期末) 将二次函数y=2x²﹣1的图象沿y轴向上平移2个单位，所得图象对应的函数表达式为．

答案解析收藏纠错 + 选题
17. (2014·淮安) 如图，△ABD≌△CBD，若∠A=80°，∠ABC=70°，则∠ADC的度数为．

答案解析收藏纠错 + 选题
18. (2014·淮安) 如图，顺次连接边长为1的正方形ABCD四边的中点，得到四边形A₁B₁C₁D₁ ，然后顺次连接四边形A₁B₁C₁D₁四边的中点，得到四边形A₂B₂C₂D₂ ，再顺次连接四边形A₂B₂C₂D₂四边的中点，得到四边形A₃B₃C₃D₃ ， …，按此方法得到的四边形A₈B₈C₈D₈的周长为．

答案解析收藏纠错 + 选题

三、解答题

19. (2014·淮安) 计算：
1. （1） 3²﹣|﹣2|﹣（π﹣3）⁰+ $\text{[math]}$ ；
2. （2）（1+ $\text{[math]}$ ）÷ $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2014·淮安) 解方程组： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2014·淮安) 如图，在三角形纸片ABC中，AD平分∠BAC，将△ABC折叠，使点A与点D重合，展开后折痕分别交AB、AC于点E、F，连接DE、DF．求证：四边形AEDF是菱形．

答案解析收藏纠错 + 选题
22. (2014·淮安) 班级准备召开主题班会，现从由3名男生和2名女生所组成的班委中，随机选取两人担任主持人，求两名主持人恰为一男一女的概率．（请用“画树状图”或“列表”等方法写出过程）

答案解析收藏纠错 + 选题
23. (2021·武汉模拟) 某公司为了解员工对“六五”普法知识的知晓情况，从本公司随机选取40名员工进行普法知识考查，对考查成绩进行统计（成绩均为整数，满分100分），并依据统计数据绘制了如下尚不完整的统计表．解答下列问题：
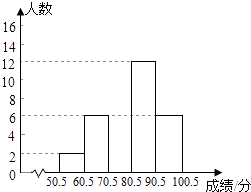
组别
分数段/分
频数/人数
频率
1
50.5～60.5
2
a
2
60.5～70.5
6
0.15
3
70.5～80.5
b
c
4
80.5～90.5
12
0.30
5
90.5～100.5
6
0.15
合计
40
1.00
1. （1）表中a=，b=，c=；
2. （2）请补全频数分布直方图；
3. （3）该公司共有员工3000人，若考查成绩80分以上（不含80分）为优秀，试估计该公司员工“六五”普法知识知晓程度达到优秀的人数．
答案解析收藏纠错 + 选题
24. (2014·淮安) 为了对一棵倾斜的古杉树AB进行保护，需测量其长度．如图，在地面上选取一点C，测得∠ACB=45°，AC=24m，∠BAC=66.5°，求这棵古杉树AB的长度．（结果取整数）
参考数据： $\text{[math]}$ ≈1.41，sin66.5°≈0.92，cos66.5°≈0.40，tan66.5°≈2.30．

答案解析收藏纠错 + 选题
25. (2023九上·新会期末) 用长为32米的篱笆围一个矩形养鸡场，设围成的矩形一边长为x米，面积为y平方米．
1. （1）求y关于x的函数关系式；
2. （2）当x为何值时，围成的养鸡场面积为60平方米？
3. （3）能否围成面积为70平方米的养鸡场？如果能，请求出其边长；如果不能，请说明理由．
答案解析收藏纠错 + 选题
26. (2014·淮安) 如图，在△ABC中，AC=BC，AB是⊙C的切线，切点为D，直线AC交⊙C于点E、F，且CF= $\text{[math]}$ AC．
1. （1）求∠ACB的度数；
2. （2）若AC=8，求△ABF的面积．
答案解析收藏纠错 + 选题
27. (2014·淮安)
如图，点A（1，6）和点M（m，n）都在反比例函数y= $\text{[math]}$ （x＞0）的图象上，
1. （1） k的值为；
2. （2）当m=3，求直线AM的解析式；
3. （3）当m＞1时，过点M作MP⊥x轴，垂足为P，过点A作AB⊥y轴，垂足为B，试判断直线BP与直线AM的位置关系，并说明理由．
答案解析收藏纠错 + 选题
28. (2014·淮安)
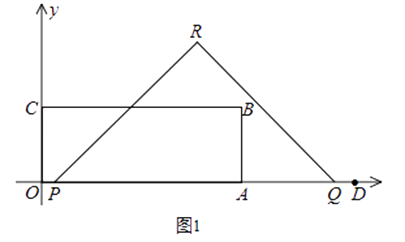
如图1，矩形OABC顶点B的坐标为（8，3），定点D的坐标为（12，0），动点P从点O出发，以每秒2个单位长度的速度沿x轴的正方向匀速运动，动点Q从点D出发，以每秒1个单位长度的速度沿x轴的负方向匀速运动，PQ两点同时运动，相遇时停止．在运动过程中，以PQ为斜边在x轴上方作等腰直角三角形PQR．设运动时间为t秒．
1. （1）当t=时，△PQR的边QR经过点B；
2. （2）设△PQR和矩形OABC重叠部分的面积为S，求S关于t的函数关系式；
3. （3）
  如图2，过定点E（5，0）作EF⊥BC，垂足为F，当△PQR的顶点R落在矩形OABC的内部时，过点R作x轴、y轴的平行线，分别交EF、BC于点M、N，若∠MAN=45°，求t的值．
答案解析收藏纠错 + 选题