湖北省武汉市2021年数学中考模拟试卷（4月）

更新时间：2021-05-20 浏览次数：183 类型：中考模拟

一、单选题

1. (2024·巴中模拟) 实数﹣2的负倒数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . ﹣2

答案解析收藏纠错 + 选题
2. (2021·岳阳模拟) 式子 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是（）

A . x≥0 B . x≥﹣1 C . x≥1 D . x≤﹣1

答案解析收藏纠错 + 选题
3. (2021·武汉模拟) 下列事件是随机事件的是（）

A . 从装有2个红球、2个黄球的袋中摸出3个球，至少有一个红球 B . 通常温度降到0℃以下，纯净的水结冰 C . 任意画一个三角形，其内角和是360° D . 随意翻到一本书的某页，这页的页码是奇数

答案解析收藏纠错 + 选题
4. (2022八下·杭州期中) 下列医护图案既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2021·柳北模拟)
如图，是由一个圆柱体和一个长方体组成的几何体．其主视图是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2021·武汉模拟) 有5张看上去无差别的卡片，上面分别写着1，2，3，4，5，随机抽取3张，用抽到的三个数字作为边长，恰能构成三角形的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021·武汉模拟) 在反比例函数 $\text{[math]}$ 图象上有两点A（ $\text{[math]}$ ， $\text{[math]}$ ）B（ $\text{[math]}$ ， $\text{[math]}$ ）， $\text{[math]}$ ＜0＜ $\text{[math]}$ ， $\text{[math]}$ ＜ $\text{[math]}$ ，则m的取值范围是（）

A . m＞ $\text{[math]}$ B . m＜ $\text{[math]}$ C . m≥ $\text{[math]}$ D . m≤ $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021·武汉模拟) 下图中的图象（折线 $\text{[math]}$ ）描述的是汽车在一直线公路上行驶时，汽车离出发地的距离 $\text{[math]}$ 千米和行驶时间 $\text{[math]}$ 小时之间的变化关系.根据图中提供的信息，判断下列说法：①汽车共行驶了120千米；②汽车在行驶途中停留了0.5小时；③汽车在整个行驶过程中的平均速度为 $\text{[math]}$ 千米/时；④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
9. (2021·武汉模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 其周长为20，⊙I是 $\text{[math]}$ 的内切圆，其半径为 $\text{[math]}$ ，则 $\text{[math]}$ 的外接圆半径为（）

A . 7 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021·武汉模拟) 古希腊数学家把数1，3，6，10，15，21，…叫做三角形数，它有一定的规律性，若把一个三角形数记为a₁ ，第二个三角形数记为a₂ ， …第n个三角形数记为a_n ，计算a₂﹣a₁ ， a₃﹣a₂ ， a₄﹣a₃ ， …，此推算，a₁₀₀﹣a₉₉＝（）

A . 99 B . 1 C . 101 D . 100

答案解析收藏纠错 + 选题

二、填空题

11. (2024八下·丰都县月考) 计算： $\text{[math]}$ =．

答案解析收藏纠错 + 选题
12. (2021·武汉模拟) 一个射手连续射靶22次，其中3次射中10环，7次射中9环，9次射中8环，3次射中7环.则射中环数的中位数和众数分别为，.

答案解析收藏纠错 + 选题
13. (2021·武汉模拟) 计算：（ $\text{[math]}$ ）÷（ $\text{[math]}$ ）＝.

答案解析收藏纠错 + 选题
14. (2021·武汉模拟) 矩形ABCD中，AB＝4，BC＝6，点E为BC的中点，沿AE将△AEB翻折得到△AFE，sin∠FCE＝.

答案解析收藏纠错 + 选题
15. (2021·武汉模拟) 抛物线 $\text{[math]}$ 图象如图，下列结论中正确的是（填序号即可）
① $\text{[math]}$ ；②不等式 $\text{[math]}$ 的解为 $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2021·武汉模拟) 如图，△ABC中，AB=8，AC=2，∠BAC的外角平分线交BC延长线于点E，BD⊥AE于D，若AE=AC，则AD的长为.

答案解析收藏纠错 + 选题

三、解答题

17. (2021·武汉模拟) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2021·武汉模拟) 已知：如图，点E、C在线段BF上，BE＝CF，AB∥DE，AC∥DF.求证：△ABC≌△DEF.

答案解析收藏纠错 + 选题
19. (2021·武汉模拟) 某公司为了解员工对“六五”普法知识的知晓情况，从本公司随机选取40名员工进行普法知识考查，对考查成绩进行统计（成绩均为整数，满分100分），并依据统计数据绘制了如下尚不完整的统计表．解答下列问题：
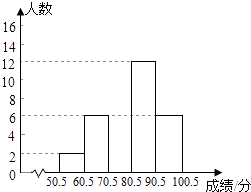
组别
分数段/分
频数/人数
频率
1
50.5～60.5
2
a
2
60.5～70.5
6
0.15
3
70.5～80.5
b
c
4
80.5～90.5
12
0.30
5
90.5～100.5
6
0.15
合计
40
1.00
1. （1）表中a=，b=，c=；
2. （2）请补全频数分布直方图；
3. （3）该公司共有员工3000人，若考查成绩80分以上（不含80分）为优秀，试估计该公司员工“六五”普法知识知晓程度达到优秀的人数．
答案解析收藏纠错 + 选题
20. (2021·武汉模拟) 如图，在下列10×10的网格中，横、纵坐标均为整数的点叫做格点，例如A(3，0)，B(4，3)都是格点.将△AOB绕点O顺时针旋转90°得到△COD（点A，B的对应点分别为点C，D）.
1. （1）作出△COD；
2. （2）下面仅用无刻度的直尺画△AOD的内心I，操作如下：
  第一步：在x轴上找一格点E，连接DE，使OE=OD；
  
  第二步：在DE上找一点F，连接OF，使OF平分∠AOD；
  
  第三步：找格点G，得到正方形OAGC，连接AC，则AC与OF的交点I是△OAD的内心.
  
  请你按步骤完成作图，并直接写出E，F，I三点的坐标.
答案解析收藏纠错 + 选题
21. (2021·武汉模拟) 如图，AC为⊙O的直径，AB＝BD，BD交AC于F，BE//AD交AC的延长线于E点.
1. （1）求证：BE为⊙O的切线；
2. （2）若AF＝4CF，求tan∠E.
答案解析收藏纠错 + 选题
22. (2021·武汉模拟) 某超市拟于中秋节前50天里销售某品牌月饼，其进价为18元/kg.设第x天的销售价格为y（元/kg）销售量为m（kg）.该超市根据以往的销售经验得出以下的销售规律：①y与x满足一次函数关系，且当x＝32时，y＝39；x＝40时，y＝35.②m与x的关系为m＝5x+50.
1. （1） y与x的关系式为；
2. （2）当34≤x≤50时，求第几天的销售利润W（元）最大？最大利润为多少？
3. （3）若在当天销售价格的基础上涨a元/kg（0＜a＜10），在第31天至42天销售利润最大值为6250元，求a的值.
答案解析收藏纠错 + 选题
23. (2021·武汉模拟) 在等腰Rt△ABC中，CA＝BA，∠CAB＝90°，点M是AB上一点.
1. （1）点N为BC上一点，满足∠CNM＝∠ANB.
  
  ①如图1，求证： $\text{[math]}$ ；
  
  ②如图2，若点M是AB的中点，连接CM，求 $\text{[math]}$ 的值；
2. （2）如图3，点P为射线CA（除点C外）上一个动点，直线PM交射线CB于点D，若AM＝1，BM＝2，直接写出△CPD的面积的最小值为.
答案解析收藏纠错 + 选题
24. (2021·武汉模拟) 抛物线y＝ax²＋c与x轴交于A、B两点，顶点为C，点P在抛物线上，且位于x轴下方．
1. （1）如图1，若P（1，－3）、B（4，0），
  ① 求该抛物线的解析式；
  
  ② 若D是抛物线上一点，满足∠DPO＝∠POB，求点D的坐标；
2. （2）如图2，已知直线PA、PB与y轴分别交于E、F两点．当点P运动时， $\text{[math]}$ 是否为定值？若是，试求出该定值；若不是，请说明理由．
答案解析收藏纠错 + 选题