2014年江苏省连云港市中考数学试卷

更新时间：2024-07-12 浏览次数：971 类型：中考真卷

一、单项选择题

1. (2014·连云港) 下列实数中，是无理数的为（）

A . ﹣1 B . ﹣ $\text{[math]}$ C . $\text{[math]}$ D . 3.14

答案解析收藏纠错 + 选题
2. (2024八下·蒙阴月考) 计算 $\text{[math]}$ 的结果是（）

A . ﹣3 B . 3 C . ﹣9 D . 9

答案解析收藏纠错 + 选题
3. (2014·连云港) 在平面直角坐标系内，点P（﹣2，3）关于原点的对称点Q的坐标为（）

A . （2，﹣3） B . （2，3） C . （3，﹣2） D . （﹣2，﹣3）

答案解析收藏纠错 + 选题
4. (2014·连云港) “丝绸之路”经济带首个实体平台﹣﹣中哈物流合作基地在我市投入使用，其年最大装卸能力达410000标箱．其中“410000”用科学记数法表示为（）

A . 0.41×10⁶ B . 4.1×10⁵ C . 41×10⁴ D . 4.1×10⁴

答案解析收藏纠错 + 选题
5. (2014·连云港) 一组数据1，3，6，1，2的众数和中位数分别是（）

A . 1，6 B . 1，1 C . 2，1 D . 1，2

答案解析收藏纠错 + 选题
6. (2019·天宁模拟) 如图，若△ABC和△DEF的面积分别为S₁、S₂ ，则（）

A . S₁= $\text{[math]}$ S₂ B . S₁= $\text{[math]}$ S₂ C . S₁=S₂ D . S₁= $\text{[math]}$ S₂

答案解析收藏纠错 + 选题
7. (2014·连云港) 如图，点P在以AB为直径的半圆内，连接AP、BP，并延长分别交半圆于点C、D，连接AD、BC并延长交于点F，作直线PF，下列说法一定正确的是（）
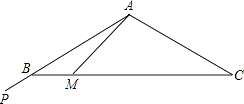
①AC垂直平分BF；②AC平分∠BAF；③FP⊥AB；④BD⊥AF．

A . ①③ B . ①④ C . ②④ D . ③④

答案解析收藏纠错 + 选题
8. (2014·连云港) 如图，△ABC的三个顶点分别为A（1，2），B（2，5），C（6，1）．若函数y= $\text{[math]}$ 在第一象限内的图象与△ABC有交点，则k的取值范围是（）

A . 2≤k≤ $\text{[math]}$ B . 6≤k≤10 C . 2≤k≤6 D . 2≤k≤ $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2024九下·龙湖模拟) 使 $\text{[math]}$ 有意义的x的取值范围是．

答案解析收藏纠错 + 选题
10. (2014·连云港) 计算：（2x+1）（x﹣3）=．

答案解析收藏纠错 + 选题
11. (2014·连云港) 一个正多边形的一个外角等于30°，则这个正多边形的边数为．

答案解析收藏纠错 + 选题
12. (2014·连云港) 若ab=3，a﹣2b=5，则a²b﹣2ab²的值是．

答案解析收藏纠错 + 选题
13. (2014·连云港) 若函数y= $\text{[math]}$ 的图象在同一象限内，y随x增大而增大，则m的值可以是（写出一个即可）．

答案解析收藏纠错 + 选题
14. (2014·连云港) 如图，AB∥CD，∠1=62°，FG平分∠EFD，则∠2=．

答案解析收藏纠错 + 选题
15. (2014·连云港) 如图1，折线段AOB将面积为S的⊙O分成两个扇形，大扇形、小扇形的面积分别为S₁、S₂ ，若 $\text{[math]}$ =0.618，则称分成的小扇形为“黄金扇形”．生活中的折扇（如图2）大致是“黄金扇形”，则“黄金扇形”的圆心角约为°．（精确到0.1）

答案解析收藏纠错 + 选题
16. (2014·连云港) 如图1，将正方形纸片ABCD对折，使AB与CD重合，折痕为EF．如图2，展开后再折叠一次，使点C与点E重合，折痕为GH，点B的对应点为点M，EM交AB于N，则tan∠ANE=．

答案解析收藏纠错 + 选题

三、解答题

17. (2024九下·泉港模拟) 计算|﹣5|+ $\text{[math]}$ ﹣（ $\text{[math]}$ ）^﹣¹ ．

答案解析收藏纠错 + 选题
18. (2014·连云港) 解不等式2（x﹣1）+5＜3x，并把解集在数轴上表示出来．

答案解析收藏纠错 + 选题
19. (2021八上·克东期末) 解方程： $\text{[math]}$ +3= $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2014·连云港) 我市启动了第二届“美丽港城，美在阅读”全民阅读活动，为了解市民每天的阅读时间情况，随机抽取了部分市民进行调查，根据调查结果绘制如下尚不完整的频数分布表：
阅读时间
x（min）
0≤x＜30
30≤x＜60
60≤x＜90
x≥90
合计
频数
450
400

50

频率

0.4
0.1

1
1. （1）补全表格；
2. （2）将每天阅读时间不低于60min的市民称为“阅读爱好者”，若我市约有500万人，请估计我市能称为“阅读爱好者”的市民约有多少万人？
答案解析收藏纠错 + 选题
21. (2020八下·庐江期中) 如图，矩形ABCD的对角线AC、BD相交于点O，DE∥AC，CE∥BD．
1. （1）求证：四边形OCED为菱形；
2. （2）连接AE、BE，AE与BE相等吗？请说明理由．
答案解析收藏纠错 + 选题
22. (2014·连云港) 如图1，在一个不透明的袋中装有四个球，分别标有字母A、B、C、D，这些球除了所标字母外都相同，另外，有一面白色、另一面黑色、大小相同的4张正方形卡片，每张卡片上面的字母相同，分别标有A、B、C、D．最初，摆成图2的样子，A、D是黑色，B、C是白色．
操作：①从袋中任意取一个球；
②将与取出球所标字母相同的卡片翻过来；
③将取出的球放回袋中
再次操作后，观察卡片的颜色．
（如：第一次取出球A，第二次取出球B，此时卡片的颜色变）
1. （1）求四张卡片变成相同颜色的概率；
2. （2）求四张卡片变成两黑两白，并恰好形成各自颜色矩形的概率．
答案解析收藏纠错 + 选题
23. (2021八上·雁塔月考) 小林在某商店购买商品A、B共三次，只有一次购买时，商品A、B同时打折，其余两次均按标价购买，三次购买商品A、B的数量和费用如下表：

购买商品A的数量（个）
购买商品B的数量（个）
购买总费用（元）
第一次购物
6
5
1140
第二次购物
3
7
1110
第三次购物
9
8
1062
1. （1）小林以折扣价购买商品A、B是第次购物；
2. （2）求出商品A、B的标价；
3. （3）若商品A、B的折扣相同，问商店是打几折出售这两种商品的？
答案解析收藏纠错 + 选题
24. (2014·连云港) 在一次科技活动中，小明进行了模拟雷达扫描实验．如图，表盘是△ABC，其中AB=AC，∠BAC=120°，在点A处有一束红外光线AP，从AB开始，绕点A逆时针匀速旋转，每秒钟旋转15°，到达AC后立即以相同旋转速度返回AB，到达后立即重复上述旋转过程．小明通过实验发现，光线从AB处旋转开始计时，旋转1秒，此时光线AP交BC边于点M，BM的长为（20 $\text{[math]}$ ﹣20）cm．
1. （1）求AB的长；
2. （2）从AB处旋转开始计时，若旋转6秒，此时光线AP与BC边的交点在什么位置？若旋转2014秒，交点又在什么位置？请说明理由．
答案解析收藏纠错 + 选题
25. (2014·连云港) 为了考察冰川的融化状况，一支科考队在某冰川上设定一个以大本营O为圆心，半径为4km的圆形考察区域，线段P₁P₂是冰川的部分边界线（不考虑其它边界），当冰川融化时，边界线沿着与其垂直的方向朝考察区域平行移动，若经过n年，冰川的边界线P₁P₂移动的距离为s（km），并且s与n（n为正整数）的关系是s= $\text{[math]}$ n²﹣ $\text{[math]}$ n+ $\text{[math]}$ ．以O为原点，建立如图所示的平面直角坐标系，其中P₁、P₂的坐标分别为（﹣4，9）、（﹣13、﹣3）．
1. （1）求线段P₁P₂所在直线对应的函数关系式；
2. （2）求冰川边界线移动到考察区域所需的最短时间．
答案解析收藏纠错 + 选题
26. (2014·连云港) 已知二次函数y=x²+bx+c，其图象抛物线交x轴于点A（1，0），B（3，0），交y轴于点C，直线l过点C，且交抛物线于另一点E（点E不与点A、B重合）．
1. （1）求此二次函数关系式；
2. （2）若直线l₁经过抛物线顶点D，交x轴于点F，且l₁∥l，则以点C、D、E、F为顶点的四边形能否为平行四边形？若能，求出点E的坐标；若不能，请说明理由．
3. （3）
  若过点A作AG⊥x轴，交直线l于点G，连接OG、BE，试证明OG∥BE．
答案解析收藏纠错 + 选题
27. (2014·连云港)
某数学兴趣小组对线段上的动点问题进行探究，已知AB=8．
问题思考：
如图1，点P为线段AB上的一个动点，分别以AP、BP为边在同侧作正方形APDC、BPEF．
1. （1）当点P运动时，这两个正方形的面积之和是定值吗？若是，请求出；若不是，请求出这两个正方形面积之和的最小值．
2. （2）分别连接AD、DF、AF，AF交DP于点K，当点P运动时，在△APK、△ADK、△DFK中，是否存在两个面积始终相等的三角形？请说明理由．
  问题拓展：
3. （3）
  如图2，以AB为边作正方形ABCD，动点P、Q在正方形ABCD的边上运动，且PQ=8．若点P从点A出发，沿A→B→C→D的线路，向点D运动，求点P从A到D的运动过程中，PQ的中点O所经过的路径的长．
4. （4）
  如图3，在“问题思考”中，若点M、N是线段AB上的两点，且AM=BN=1，点G、H分别是边CD、EF的中点，请直接写出点P从M到N的运动过程中，GH的中点O所经过的路径的长及OM+OB的最小值．
答案解析收藏纠错 + 选题