广东省深圳市七校联合体2019届高三理数冲刺模拟试卷

更新时间：2024-07-13 浏览次数：538 类型：高考模拟

一、选择题：本大题共12个小题,每小题5分,共60分．

1. (2019·深圳模拟) 已知 $\text{[math]}$ 为实数集，集合 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019·深圳模拟) 复数 $\text{[math]}$ （其中 $\text{[math]}$ 为虚数单位）， $\text{[math]}$ 为 $\text{[math]}$ 的共轭复数，则 $\text{[math]}$ 的虚部是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2019·深圳模拟) 已知实数 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值是（）

A . 6 B . 4 C . 2 D . 0

答案解析收藏纠错 + 选题
4. (2019·深圳模拟) 下列说法正确的是（）

A . 命题“若 $\text{[math]}$ ，则 $\text{[math]}$ .”的否命题是“若 $\text{[math]}$ ，则 $\text{[math]}$ .” B . $\text{[math]}$ 是函数 $\text{[math]}$ 在定义域上单调递增的充分不必要条件 C . $\text{[math]}$ D . 若命题 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2019·深圳模拟) 已知 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2019·深圳模拟) 函数 $\text{[math]}$ 的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2019·深圳模拟) 若将函数 $\text{[math]}$ 的图象向左平移 $\text{[math]}$ （ $\text{[math]}$ ）个单位，所得图象关于原点对称，则 $\text{[math]}$ 最小时， $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2019·深圳模拟) 现行普通高中生在高一升高二时面临着选文理的问题，某校抽取了部分男、女生意愿的一份样本，制作出如下两个等高条形图：根据这两幅图中的信息，下列哪个统计结论是不正确的（）

A . 样本中的女生数量多于男生数量 B . 样本中有理意愿的生数量多于有文意愿的生数量 C . 样本中的男生偏爱理 D . 样本中的女生偏爱文

答案解析收藏纠错 + 选题
9. (2019·深圳模拟) 某空间几何体的三视图如图所示，则该几何体的体积为（）

A . 1 B . 2 C . 4 D . 8

答案解析收藏纠错 + 选题
10. (2019·深圳模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ 为斜边 $\text{[math]}$ 边的高，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2019·深圳模拟) 已知双曲线 $\text{[math]}$ ： $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）的一条渐近线为 $\text{[math]}$ ，圆 $\text{[math]}$ ： $\text{[math]}$ 与 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点，若 $\text{[math]}$ 是等腰直角三角形，且 $\text{[math]}$ （其中 $\text{[math]}$ 为坐标原点），则双曲线 $\text{[math]}$ 的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2019·深圳模拟) 若函数 $\text{[math]}$ 在 $\text{[math]}$ 单调递增，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题5分，满分20分）

13. (2019·深圳模拟) $\text{[math]}$ 展开式中的常数项为 $\text{[math]}$ ,则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2019·深圳模拟) 若直线 $\text{[math]}$ 与曲线 $\text{[math]}$ 相切，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2019·深圳模拟) 有3女2男共5名志愿者要全部分到3个社区去参加志愿服务，每个社区1到2人，甲、乙两名女志愿者需到同一社区，男志愿者到不同社区，则不同的分法种数为．

答案解析收藏纠错 + 选题
16. (2019·深圳模拟) 已知点 $\text{[math]}$ ，抛物线 $\text{[math]}$ ： $\text{[math]}$ （ $\text{[math]}$ ）的准线为 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上，作 $\text{[math]}$ 于 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题（本大题共6小题，共70分．）

17. (2019·深圳模拟) 设 $\text{[math]}$ 为等差数列 $\text{[math]}$ 的前n项和，已知 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的通项公式；
2. （2）令 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 对一切 $\text{[math]}$ 成立，求实数m的最小值．
答案解析收藏纠错 + 选题
18. (2019·深圳模拟) 如图，在底面为菱形的四棱锥P-ABCD中， $\text{[math]}$ ，点E在PD上，且 $\text{[math]}$ ．

（Ⅰ）求证： $\text{[math]}$ 平面ABCD；

（Ⅱ）求二面角E-AC-D的正弦值；

（Ⅲ）在棱PC上是否存在点F使得 $\text{[math]}$ 平面EAC？若存在，试求PF的值；若不存在，请说明理由．

答案解析收藏纠错 + 选题
19. (2019·深圳模拟) 某保险公司针对企业职工推出一款意外险产品，每年每人只要交少量保费，发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三类工种，根据历史数据统计出三类工种的每赔付频率如下表（并以此估计赔付概率）.

（Ⅰ）根据规定，该产品各工种保单的期望利润都不得超过保费的20%，试分别确定各类工种每张保单保费的上限；

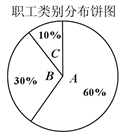
（Ⅱ）某企业共有职工20000人，从事三类工种的人数分布比例如图，老板准备为全体职工每人购买一份此种保险，并以（ Ⅰ）中计算的各类保险上限购买，试估计保险公司在这宗交易中的期望利润.

答案解析收藏纠错 + 选题
20. (2019·深圳模拟) 已知椭圆 $\text{[math]}$ $\text{[math]}$ （ $\text{[math]}$ ）的两个焦点与短轴的一个端点是有一个角为 $\text{[math]}$ 的等腰三角形的三个顶点，直线 $\text{[math]}$ ： $\text{[math]}$ 与椭圆 $\text{[math]}$ 有且只有一个公共点 $\text{[math]}$ ．
（Ⅰ）求椭圆 $\text{[math]}$ 的方程及点 $\text{[math]}$ 的坐标；

（Ⅱ）斜率为 $\text{[math]}$ 的直线 $\text{[math]}$ 与椭圆 $\text{[math]}$ 交于不同的两点 $\text{[math]}$ 、 $\text{[math]}$ ，且与直线 $\text{[math]}$ 交于点 $\text{[math]}$ ，证明：存在常数 $\text{[math]}$ ，使得 $\text{[math]}$ 成立，并求 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
21. (2019·深圳模拟) 定义在R上的函数f (x)满足 $\text{[math]}$ $\text{[math]}$ .
(Ⅰ)求函数f (x)的解析式；

(Ⅱ)求函数g (x)的单调区间；

(Ⅲ)如果s、t、r满足 $\text{[math]}$ ，那么称s比t更靠近r ．当a≥2且x≥1时，试比较 $\text{[math]}$ 和 $\text{[math]}$ 哪个更靠近lnx ，并说明理由．

答案解析收藏纠错 + 选题
22. (2019·深圳模拟) 在平面直角坐标系 $\text{[math]}$ 中，曲线 $\text{[math]}$ ： $\text{[math]}$ ，曲线 $\text{[math]}$ ： $\text{[math]}$ （ $\text{[math]}$ 为参数），以坐标原点 $\text{[math]}$ 为极点， $\text{[math]}$ 轴正半轴为极轴，建立极坐标系.
（Ⅰ）求曲线 $\text{[math]}$ ， $\text{[math]}$ 的极坐标方程；

（Ⅱ）曲线 $\text{[math]}$ ： $\text{[math]}$ （ $\text{[math]}$ 为参数， $\text{[math]}$ ， $\text{[math]}$ ）分别交 $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 两点，当 $\text{[math]}$ 取何值时， $\text{[math]}$ 取得最大值.

答案解析收藏纠错 + 选题
23. (2019·深圳模拟) 已知函数 $\text{[math]}$ $\text{[math]}$ .
（Ⅰ）当 $\text{[math]}$ 时，求不等式 $\text{[math]}$ 的解集；

（Ⅱ）设 $\text{[math]}$ ，且存在 $\text{[math]}$ ，使得 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围.

答案解析收藏纠错 + 选题