
 B .
B . 赛组织者应邀请x个队参赛,则x满足的关系式为( )
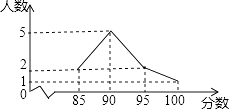


① ac>0 ②方程ax2+bx+c=0的根是x1=-1,x2=3
③a+b+c<0④当x>1时,y随x的增大而增大
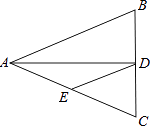
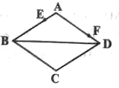
下列说法不正确的是( )

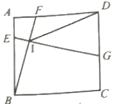

的长是 .

![]()
1=12
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+.……+(2n-1)=(n为正整数)

①第3层包括块正方形利和块正三角形地砖;
②第n层包括块正三角形地砖(用含n的代数式表示)。

|
经营类目 |
服装 |
|||
|
收费标准 |
一、技术服务费 |
每笔交易额的5% |
||
|
二、年费 |
5(万元/年) |
年销售额达到50万元,返年费的50% |
年销售额达到120万元,返还全部年费 |
|
例如,A卖家的年销售额为60万元,则实际缴纳费用60×5%+5-2.5=5.5万元。



