①当a=10时,方程组的解是 ;②当x,y的值互为相反数时,a=20;③不存在一个实数a使得x=y;④若3x-3a=35 , 则a=5
2x2·(-3x3)=.

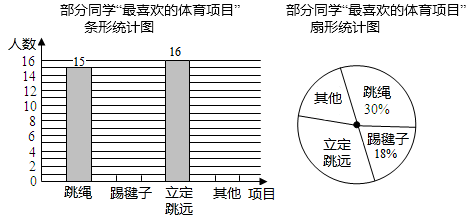
①请你设计出所有的租车方案;
②若小客车每辆租金300元,大客车每辆租金500元,请选出最省线的租车方案,并求出最少租金.
整式乘法与因式分解是方向相反的变形.如何把二次_一项式ax2+bx+c进行因式分解呢?我们已经知道,(a1x+c1)(a2x+c2)=a1a2x2+a1c2x+a2c1x+c1c2=a1a2x2+(a1c2+a2c1)x+c1c2.反过来,就得到:a1a2x2+(a1c2+a2c1)x+c1c2=(a1x+c1)(a2x+c2).
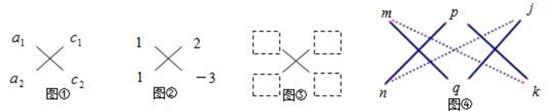
我们发现,二次项的系数a分解成a1a2 , 常数项c分解成c1c2 , 并且把a1 , a2 , c1 , c2 , 如图①所示摆放,按对角线交叉相乘再相加,就得到a1c2+a2c1 , 如果a1c2+a2c1的值正好等于ax2+bx+c的一次项系数b,那么ax2+bx+c就可以分解为(a1x+c1)(a2x+c2),其中a1 , c1位于图的上一行,a2 , c2位于下一行.
像这种借助画十字交叉图分解系数,从而帮助我们把二次三项式分解因式的方法,通常叫做“十字相乘法”.
例如,将式子x2-x-6分解因式的具体步骤为:首先把二次项的系数1分解为两个因数的积,即1=1×1,把常数项-6也分解为两个因数的积,即-6=2×(-3);然后把1,1,2,-3按图②所示的摆放,按对角线交叉相乘再相加的方法,得到1×(-3)+1×2=-1,恰好等于一次项的系数-1,于是x2-x-6就可以分解为(x+2)(x-3).
请你仔细体会上述方法,并尝试对下面两个二次三项式进行分解因式:
Ⅰ.2x2+5x-7=;
Ⅱ.6x2-7xy+2y2= .
对于形如ax2+bxy+cy2+dx+ey+f的关于x,y的二元二次多项式也可以用“十字相乘法”来分解.如图④,将a分解成mn乘积作为一列,c分解成pq乘积作为第二列,f分解成jk乘积作为第三列,如果mq+np=b,pk+qj=e,mk+nj=d,即第1,2列、第2,3列和第1,3列都满足十字相乘规则,则原式=(mx+py+j)(nx+qy+k),请你认真阅读上述材料并尝试挑战下列问题:
Ⅰ.分解因式3x2+5xy-2y2+x+9y-4= .
Ⅱ.若关于x,y的二元二次式x2+7xy-18y2-5x+my-24 可以分解成两个一次因式的积,求m的值.
Ⅲ.已知x,y为整数,且满足x2+3xy+2y2+2x+3y=-1,请写出一组符合题意的x,y的值.