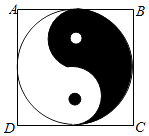
如图,正方形ABCD内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
 B .
B .  C .
C .  D .
D . 
 B .
B . 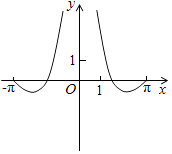 C .
C . 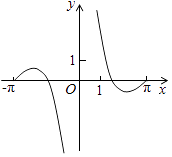 D .
D . 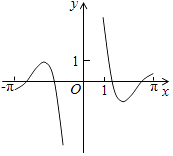

抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
零件尺寸 | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
零件尺寸 | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得 =
xi=9.97,s=
=
=0.212,
≈18.439,
(xi﹣
)(i﹣8.5)=﹣2.78,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
(ⅰ)从这一天抽检的结果看,是否需对当天的生产过程进行检查?
(ⅱ)在( ﹣3s,
+3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
附:样本(xi , yi)(i=1,2,…,n)的相关系数r= ,
≈0.09.
在直角坐标系xOy中,曲线C的参数方程为 (θ为参数),直线l的参数方程为
(t为参数).