
 B .
B .  C .
C .  D .
D . 
|
星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
|
最高气温 |
4℃ |
5℃ |
3℃ |
4℃ |
3℃ |
﹣2℃ |
﹣2℃ |
|
最低气温 |
﹣13℃ |
﹣13℃ |
﹣13℃ |
﹣9℃ |
﹣11℃ |
﹣13℃ |
﹣15℃ |
则这周内温差最大的一天是星期.
2△5=2×3+5=11,2△(﹣1)=2×3+(﹣1)=5,
6△3=6×3+3=21,4△(﹣3)=4×3+(﹣3)=9……
根据这个定义,计算(﹣2018)△2018的结果为

|
星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
|
分拣情况(单位:万件) |
+6 |
﹣3 |
﹣4 |
+5 |
﹣1 |
+7 |
﹣8 |
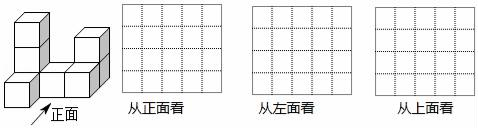
方案一:买一副乒乓球拍送一盒兵兵球;
方案二:乒乓球拍和乒乓球都按定价的90%付款.
某客户要到该体育用品商店购买乒乓球拍10副,兵兵球x盒(x>10).
问题情境:在棱长为1的正方体右侧拼搭若干个棱长小于或等于1的其它正方体,使拼成的立体图形为一个长方体.如图1,是两个棱长为1的正方体搭成的长方体,图2是从上面看这个长方体得到的平面图形,它由两个正方形组成.

操作探究:
请从A,B两题中任选一题作答,我选择哪题.
A.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形)
B.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形,并在所画图形的下方直接写出拼成该长方体所需的正方体的总个数)
阅读材料:
数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示;
在数轴上,有理数3与1对应的两点之间的距离为|3﹣1|=2;
在数轴上,有理数5与﹣2对应的两点之间的距离为|5﹣(﹣2)|=7;
在数轴上,有理数﹣2与3对应的两点之间的距离为|﹣2﹣3|=5;
在数轴上,有理数﹣8与﹣5对应的两点之间的距离为|﹣8﹣(﹣5)|=3;……
如图1,在数轴上有理数a对应的点为点A,有理数b对应的点为点B,A,B两点之间的距离表示为|a﹣b|或|b﹣a|,记为|AB|=|a﹣b|=|b﹣a|.

解决问题:
如图2,点M,N,P是数轴上的三点,点M表示的数为4,点N表示的数为﹣2,动点P表示的数为x.
请从A,B两题中任选一题作答,我选择题.

A.①若点P在点M,N两点之间,则|PM|+|PN|=;
②若|PM|=2|PN|,即点P到点M的距离等于点P到点N的距离的2倍,则x等于.
B.①若点P在点M,N之间,则|x+2|+|x﹣4|=;
若|x+2|+|x﹣4|═10,则x=;
②根据阅读材料及上述各题的解答方法,|x+2|+|x|+|x﹣2|+|x﹣4|的最小值等于.