2017年四川省成都市成华区中考数学二诊试卷

更新时间：2017-07-07 浏览次数：1398 类型：中考模拟

一、选择题

1. (2017·成华模拟) 在2， $\text{[math]}$ ，0，﹣2四个数中，最大的一个数是（）

A . 2 B . $\text{[math]}$ C . 0 D . ﹣2

答案解析收藏纠错 + 选题
2. (2019九下·保山期中) 下面所给几何体的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2017·临沂模拟) 下列运算正确的是（）

A . （a﹣3）²=a²﹣9 B . a²•a⁴=a⁸ C . $\text{[math]}$ =±3 D . $\text{[math]}$ =﹣2

答案解析收藏纠错 + 选题
4. (2017七下·淅川期末) 下列交通标志中，是轴对称图形但不是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2017·枣阳模拟) 如图，AB∥CD，AE平分∠CAB交CD于点E，若∠C=50°，则∠AED=（）

A . 65° B . 115° C . 125° D . 130°

答案解析收藏纠错 + 选题
6. (2024八下·杭州期末) 一元二次方程x²﹣6x﹣5=0配方可变形为（）

A . （x﹣3）²=14 B . （x﹣3）²=4 C . （x+3）²=14 D . （x+3）²=4

答案解析收藏纠错 + 选题
7. (2017·成华模拟) 已知关于x的方程x²+2x﹣（m﹣2）=0有两个不相等的实数根，则m的取值范围是（）

A . m≥1 B . m≤1 C . m＞1 D . m＜1

答案解析收藏纠错 + 选题
8. 如图，点A、B、C、D在⊙O上，DE⊥OA，DF⊥OB，垂足分别为E，F，若∠EDF=50°，则∠C的度数为（）

A . 40° B . 50° C . 65° D . 130°

答案解析收藏纠错 + 选题
9. (2017·成华模拟) 二次函数y=ax²+bx+c（a≠0）的图象如图所示，下列结论：①a＜0；②c＞0；③a﹣b+c＜0；④b²﹣4ac＞0，其中正确的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题

10. (2017·成华模拟) 因式分解：a²﹣9=．

答案解析收藏纠错 + 选题
11. (2024八下·周口月考) 函数 $\text{[math]}$ 中，自变量x的取值范围是．

答案解析收藏纠错 + 选题
12. (2017八下·海安期中) 如图，在菱形ABCD中，AC、BD相交于点O，E为AB的中点，若OE=2，则菱形ABCD的周长是．

答案解析收藏纠错 + 选题
13. (2017·成华模拟) 如图，在矩形ABCD中，点E在边BC上，BE=EC=2，且AE=AD，以A为圆心，AB长为半径作圆弧AE于点F，则扇形ABF的面积是（结果保留π）．

答案解析收藏纠错 + 选题

三、解答题

14. (2017·成华模拟) 计算题
1. （1）计算：|1﹣ $\text{[math]}$ |﹣3tan30°+（π﹣2017）⁰﹣（﹣ $\text{[math]}$ ）^﹣¹
2. （2）解不等式组 $\text{[math]}$ 并在数轴上表示它的解集．
答案解析收藏纠错 + 选题
15. (2017·成华模拟) 先化简（1﹣ $\text{[math]}$ ）• $\text{[math]}$ ，再在1，2，3中选取一个适当的数代入求值．

答案解析收藏纠错 + 选题
16. (2017·河北模拟)
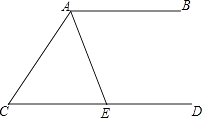
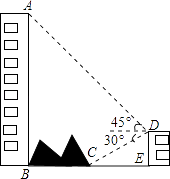
如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=80m，DE=10m，求障碍物B，C两点间的距离（结果精确到0.1m）（参考数据： $\text{[math]}$ ≈1.414， $\text{[math]}$ ≈1.732）

答案解析收藏纠错 + 选题
17. (2017·成华模拟) 在甲、乙两名同学中选拔一人参加“中华好诗词”大赛，在相同的测试条件下，两人5次测试成绩（单位：分）如下：
甲：79，86，82，85，83
乙：88，79，90，81，72．
回答下列问题：
1. （1）甲成绩的平均数是，乙成绩的平均数是；
2. （2）经计算知S_甲²=6，S_乙²=42．你认为选拔谁参加比赛更合适，说明理由；
3. （3）如果从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析，求抽到的两个人的成绩都大于80分的概率．
答案解析收藏纠错 + 选题
18. (2017·成华模拟) 如图，一次函数y=x+m的图象与反比例函数y= $\text{[math]}$ 的图象交于A，B两点，且与x轴交于点C，点A的坐标为（2，1）．
1. （1）求一次函数和反比例函数的解析式；
2. （2）求点C的坐标；
3. （3）结合图象直接写出不等式0＜x+m≤ $\text{[math]}$ 的解集．
答案解析收藏纠错 + 选题
19. (2017·成华模拟)
已知：AB为⊙O的直径，C是⊙O上一点，如图，AB=12，BC=4 $\text{[math]}$ ．BH与⊙O相切于点B，过点C作BH的平行线交AB于点E．
1. （1）求CE的长；
2. （2）延长CE到F，使EF= $\text{[math]}$ ，连接BF并延长BF交⊙O于点G，求BG的长；
3. （3）在（2）的条件下，连接GC并延长GC交BH于点D，求证：BD=BG．
答案解析收藏纠错 + 选题

四、填空题

20. (2017·成华模拟) 在平面直角坐标系xOy中，点P（4，a）在正比例函数y= $\text{[math]}$ x的图象上，则点Q（2a﹣5，a）关于y轴的对称点Q'坐标为．

答案解析收藏纠错 + 选题
21. (2017·成华模拟) 定义新运算：a*b=a（b﹣1），若a、b是关于一元二次方程x²﹣x+ $\text{[math]}$ m=0的两实数根，则b*b﹣a*a的值为．

答案解析收藏纠错 + 选题
22. (2017·成华模拟)
如图，AB是⊙O的直径，AB=10，∠A=40°，点D为弧BC的中点，点P是直径AB上的一个动点，PC+PD的最小值为．

答案解析收藏纠错 + 选题
23. (2017·成华模拟) 如图，已知双曲线y= $\text{[math]}$ 与直线y=k₂x（k₁ ， k₂都为常数）相交于A，B两点，在第一象限内双曲线y= $\text{[math]}$ 上有一点M（M在A的左侧），设直线MA，MB分别与x轴交于P，Q两点，若MA=m•AP，MB=n•QB，则n﹣m的值是．

答案解析收藏纠错 + 选题
24. (2017·成华模拟)
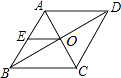
如图，在正n边形（n为整数，且n≥4）绕点A顺时针旋转60°后，发现旋转前后两图形有另一交点O，连接AO，我们称AO为“叠弦”；再将“叠弦”AO所在的直线绕点A逆时针旋转60°后，交旋转前的图形于点P，连接PO，我们称∠OAB为正n边形的“叠弦角”，△AOP为“叠弦三角形”．以下说法，正确的是．（填番号）
①在图1中，△AOB≌△AOD'；
②在图2中，正五边形的“叠弦角”的度数为360°；
③“叠弦三角形”不一定都是等边三角形； ④正n边形的“叠弦角”的度数为60°﹣ $\text{[math]}$ ．

答案解析收藏纠错 + 选题

五、解答题

25. (2017·成华模拟) 骑自行车旅行越来越受到人们的喜爱，各种品牌的山地自行车相继投放市场，某车行经营的A型车去年3月份销售总额为3.2万元，今年经过改造升级后A型车每辆销售价比去年增加400元，若今年3月份与去年3月份卖出的A型车数量相同，则今年3月份A型车销售总额将比去年3月份销售总额增加25%．
1. （1）求今年3月份A型车每辆销售价多少元？
2. （2）该车行计划今年4月份新进一批A型车和B型车共50辆，且B型车的进货数量不超过A型车数量的两倍，A、B两种型号车的进货和销售价格如下表，问应如何进货才能使这批车获利最多？
  A型车
  B型车
  进货价格（元/辆）
  1100
  1400
  销售价格（元/辆）
  今年的销售价格
  2400
答案解析收藏纠错 + 选题
26. (2017·成华模拟) 解答题
1. （1）如图1，在正方形ABCD中，点O是对角线AC的中点，点E是边BC上一点，连接OE，过点O作OE的垂线交AB于点F．求证：OE=OF．
2. （2）若将（1）中，“正方形ABCD”改为“矩形ABCD”，其他条件不变，如图2，连接EF．
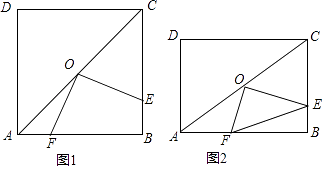
  ⅰ）求证：∠OEF=∠BAC．
  ⅱ）试探究线段AF，EF，CE之间数量上满足的关系，并说明理由．
答案解析收藏纠错 + 选题
27. (2017·成华模拟)
如图，抛物线y=ax²+bx+c（a≠0）与x轴相交于A（﹣1，0），B（3，0），与y轴交于点C（0，3）．
1. （1）求抛物线的解析式；
2. （2）连接BC，点P为抛物线上第一象限内一动点，当△BCP面积最大时，求点P的坐标；
3. （3）设点D是抛物线的对称轴上的一点，在抛物线上是否存在点Q，使以点B，C，D，Q为顶点的四边形为平行四边形？若存在，求出点Q的坐标；若不存在，说明理由．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

2017年四川省成都市成华区中考数学二诊试卷

副标题：

*注意事项：

2017年四川省成都市成华区中考数学二诊试卷

试题分析

总体分析

题量分析

难度分析

知识点分析

	A型车	B型车
进货价格（元/辆）	1100	1400
销售价格（元/辆）	今年的销售价格	2400