
甲:如图①,已知矩形ABCD和矩形EFGO在平面直角坐标系中,点B,F的坐标分别为(﹣4,4),(2,1).若矩形ABCD和矩形EFGO是位似图形,点P(点P在GC上)是位似中心,则点P的坐标为(0,2).


图① 图②
乙:如图②,正方形网格中,每个小正方形的边长是1个单位长度,以点C为位似中心,在网格中画△A1B1C1 , 使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的位似比为2:1,则点B1的坐标为(4,0).对于两人的观点,下列说法正确的是( )

按下列要求画图:以点 为位似中心,将
向
轴左侧按比例尺
放大得
的位似图形
,并解决下列问题:

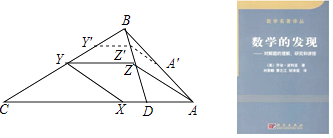
在数学中,利用图形在变化过程中的不变性质,常常可以找到解决问题的办法.著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子:请问如何在一个三角形ABC的AC和BC两边上分别取一点X和Y,使得AX=BY=XY.(如图)解决这个问题的操作步骤如下:
第一步,在CA上作出一点D,使得CD=CB,连接BD.第二步,在CB上取一点Y',作Y'Z'∥CA,交BD于点Z',并在AB上取一点A',使Z'A'=Y'Z'.第三步,过点A作AZ∥A'Z',交BD于点Z.第四步,过点Z作ZY∥AC,交BC于点Y,再过点Y作YX∥ZA,交AC于点X.
则有AX=BY=XY.
下面是该结论的部分证明:
证明:∵AZ∥A'Z',∴∠BA'Z'=∠BAZ,
又∵∠A'BZ'=∠ABZ.∴△BA'Z'~△BAZ.
∴ .
同理可得 .∴
.
∵Z'A'=Y'Z',∴ZA=YZ.
任务: