2017年湖南省株洲市中考数学试卷

如图示在△ABC中∠B=．

如图示直线y= x+ 与x轴、y轴分别交于点A、B，当直线绕着点A按顺时针方向旋转到与x轴首次重合时，点B运动的路径的长度为．

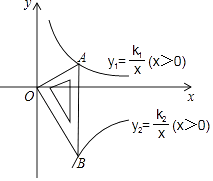
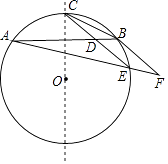
①A区域3×3阶魔方爱好者进入下一轮角逐的人数的比例（结果用最简分数表示）．

②若3×3阶魔方赛各个区域的情况大体一致，则根据A区域的统计结果估计在3×3阶魔方赛后进入下一轮角逐的人数．

③若3×3阶魔方赛A区域爱好者完成时间的平均值为8.8秒，求该项目赛该区域完成时间为8秒的爱好者的概率（结果用最简分数表示）．

①求证：△DAE≌△DCF；

②求证：△ABG∽△CFG．

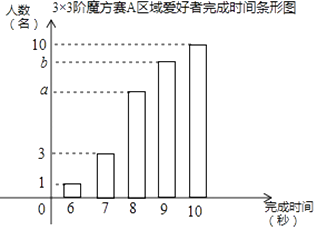
如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的俯角为α其中tanα=2 ，无人机的飞行高度AH为500 米，桥的长度为1255米．

①求点H到桥左端点P的距离； 

②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°，求这架无人机的长度AB．

①求k的值以及w关于t的表达式；  

②若用w_max和w_min分别表示函数w的最大值和最小值，令T=w_max+a²﹣a，其中a为实数，求T_min ．

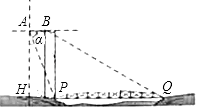
①求证：CE∥BF； 

②若BD=2，且EA：EB：EC=3：1： ， 求△BCD的面积（注：根据圆的对称性可知OC⊥AB）．

已知二次函数y=﹣x²+bx+c+1，

①当b=1时，求这个二次函数的对称轴的方程； 

②若c=- b²﹣2b，问：b为何值时，二次函数的图象与x轴相切？

③若二次函数的图象与x轴交于点A（x₁ ， 0），B（x₂ ， 0），且x₁＜x₂ ， 与y轴的正半轴交于点M，以AB为直径的半圆恰好过点M，二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F，且满足 = ，求二次函数的表达式．