2017年云南省临沧市临翔区民族中学高考数学三模试卷（理科）...

更新时间：2017-08-25 浏览次数：453 类型：高考模拟

一、选择题

1. (2017·沈阳模拟) 全集U={1，2，3，4，5，6}，集合A={x|x²﹣3x+2=0}，B={x|x=2a，a∈A}，则集合∁_U（A∪B）的子集个数为（）

A . 1 B . 3 C . 8 D . 4

答案解析收藏纠错 + 选题
2. (2017·沈阳模拟) 已知复数z=﹣2+i，则复数 $\text{[math]}$ 的模为（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
3. (2017·沈阳模拟) 已知点A（2，0），B（3，2），向量 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
4. (2017·临翔模拟) 随机变量X～N（1，4），若p（x≥2）=0.2，则p（0≤x≤1）为（）

A . 0.2 B . 0.6 C . 0.4 D . 0.3

答案解析收藏纠错 + 选题
5. (2017·临翔模拟) 已知 $\text{[math]}$ ，则 $\text{[math]}$ =（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
6. (2017·沈阳模拟) 执行如图的程序框图（N∈N^*），那么输出的p是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2017·临翔模拟) 某三棱锥的三视图如图所示，则该三棱锥的表面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2017·临翔模拟) 将函数 $\text{[math]}$ 的图象向右平移 $\text{[math]}$ 个单位后得到的图象的一个对称轴是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2017·临翔模拟) （1﹣2x）³的展开式中所有的二项式系数和为a，函数y=m^x^﹣²+1（m＞0且m≠1）经过的定点的纵坐标为b，则 $\text{[math]}$ 的展开式中x⁶y²的系数为（）

A . 320 B . 446 C . 482 D . 248

答案解析收藏纠错 + 选题
10. (2017·沈阳模拟) 下列说法正确的个数是（）
①若f（x）= $\text{[math]}$ +a为奇函数，则a= $\text{[math]}$ ；
②“在△ABC中，若sinA＞sinB，则A＞B”的逆命题是假命题；
③“三个数a，b，c成等比数列”是“b= $\text{[math]}$ ”的既不充分也不必要条件；
④命题“∀x∈R，x³﹣x²+1≤0”的否定是“∃x₀∈R，x₀³﹣x₀²+1＞0”．

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
11. (2017·临翔模拟) 已知等差数列{a_n}的公差d≠0，且a₁ ， a₃ ， a₁₃成等比数列，若a₁=1，S_n是数列{a_n}的前n项和，则 $\text{[math]}$ 的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
12. (2017·沈阳模拟) 已知焦点为F的抛物线y²=2px（p＞0）上有一点 $\text{[math]}$ ，以A为圆心，|AF|为半径的圆被y轴截得的弦长为 $\text{[math]}$ ，则m=（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2017·临翔模拟) 已知△ABC的内角A，B，C所对的边分别为a，b，c，且a=2，b=3，tanB=3，则sinA的值为

答案解析收藏纠错 + 选题
14. (2017高二下·衡水期末) 点M（x，y）是不等式组 $\text{[math]}$ 表示的平面区域Ω内的一动点，且不等式2x﹣y+m≤0恒成立，则m的取值范围是．

答案解析收藏纠错 + 选题
15. (2017·临翔模拟) 已知正四面体ABCD的棱长为2，E为棱AB的中点，过E作其外接球的截面，则截面面积的最小值为．

答案解析收藏纠错 + 选题
16. (2017·临翔模拟) 设函数y=f（x）的图象与y=2^x^﹣^a的图象关于直线y=﹣x对称，且f（﹣2）+f（﹣4）=1，则a=．

答案解析收藏纠错 + 选题

三、解答题

17. (2017·临翔模拟) 已知数列{a_n}的前n项和S_n= $\text{[math]}$ ﹣ $\text{[math]}$ （n∈N^*）．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）若b_n=a_n•log₃a_n ，求数列{b_n}的前n项和．

答案解析收藏纠错 + 选题
18. (2017·临翔模拟) 某次数学考试试题中共有10道选择题，每道选择题都有4个选项，其中仅有一个是正确的．评分标准规定：“每题只选1项，答对得5分，不答或答错得0分．”某考生每道题都给了一个答案，已确定有6道题的答案是正确的，而其余题中，有两道题都可判断出两个选项是错误的有一道题可以判断一个选项是错误的，还有一道题因不理解题意只能乱猜，试求出该考生：
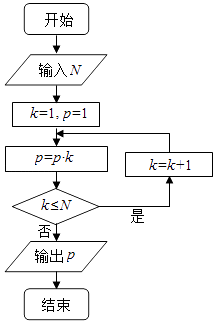
（Ⅰ）得45分的概率；
（Ⅱ）所得分数ξ的数学期望．

答案解析收藏纠错 + 选题
19. (2017·临翔模拟) 如图，在直角梯形ABCP中， $\text{[math]}$ ，D是CP的中点，将△PAD沿AD折起，使得PD⊥平面ABCD．
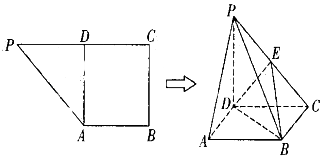
（Ⅰ）求证：平面PAD⊥平面ABCD
（Ⅱ）若E在CP上且二面角E﹣BD﹣C所成的角的余弦值为 $\text{[math]}$ ，求CE的长．

答案解析收藏纠错 + 选题
20. (2017·临翔模拟) 设椭圆C： $\text{[math]}$ =1（a＞b＞0）的焦点F₁ ， F₂ ，过右焦点F₂的直线l与C相交于P、Q两点，若△PQF₁的周长为短轴长的2 $\text{[math]}$ 倍．
（Ⅰ）求C的离心率；
（Ⅱ）设l的斜率为1，在C上是否存在一点M，使得 $\text{[math]}$ ？若存在，求出点M的坐标；若不存在，说明理由．

答案解析收藏纠错 + 选题
21. (2017·临翔模拟) 已知函数f（x）=ax²+2x﹣ln（x+1）（a为常数）
1. （1）当a=﹣1时，求函数f（x）的单调区间；
2. （2）求x∈[0，+∞）时，不等式f（x）≤x恒成立，求实数a的取值范围．
答案解析收藏纠错 + 选题
22. (2017·临翔模拟) 在直角坐标系xOy中，曲线 $\text{[math]}$ （t为参数，t≠0），其中0≤a＜π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C₂：ρ=4sinθ，曲线 $\text{[math]}$ ．
（Ⅰ）求C₂与C₃交点的直角坐标系；
（Ⅱ）若C₂与C₁相交于点A，C₃与C₁相交于点B，求|AB|的最大值．

答案解析收藏纠错 + 选题
23. (2017·临翔模拟) 设函数f（x）=|x﹣1|+2|x+1|
（Ⅰ）解不等式f（x）≤4；
（Ⅱ）当f（x）≤4时，|x+3|+|x+a|＜x+6，求实数a的取值范围．

答案解析收藏纠错 + 选题