 B .
B . 
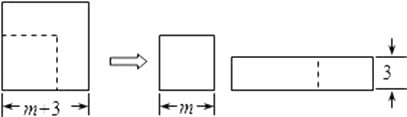
①如果某圆锥的侧面展开图是半圆,则其轴截面一定是等边三角形;
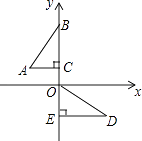
②若点A在直线y=2x﹣3上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;
③半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的点共有四个;
④若A(a,m)、B(a﹣1,n)(a>0)在反比例函y= 的图象上,则m<n.
其中,正确命题的个数是( )
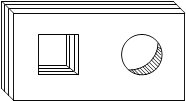

如图,已知点A是直线y=x与反比例函数y= (k>0,x>0)的交点,B是y=
图象上的另一点,BC//x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )

 B .
B . 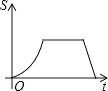 C .
C .  D .
D . 

求作△A1B1C1 , 使A1B1=AB,∠B1=∠B,B1C1=BC.
(作图要求:写已知、求作,不写作法,不证明,保留作图痕迹)
已知:
求作:


在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:
第一步:对折矩形纸片ABCD,使AD与BC重合,把纸片展开,得到折痕EF(如图1);
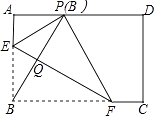
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2).

请解答以下问题:
问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°,求证:AD•BC=AP•BP;

探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.

应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠CPD=∠A,设点P的运动时间为t(秒),当DC=4BC时,求t的值.
