2017年浙江省杭州市中考数学仿真试卷（二）

更新时间：2017-07-28 浏览次数：893 类型：中考模拟

一、选择题：

1. (2024七下·儋州期末) 不等式组 $\text{[math]}$ 的正整数解的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
2. (2017·杭州模拟) 下列计算正确的是（　　）

A . 2x+x=2x² B . 2x²﹣x²=2 C . 2x²•3x²=6x⁴ D . 2x⁶÷x²=2x³

答案解析收藏纠错 + 选题
3. (2019·广东模拟) 一个袋子中装有3个红球和2个黄球，这些球的形状、大小．质地完全相同，在看不到球的条件下，随机从袋子里同时摸出2个球，其中2个球的颜色相同的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020·陕西模拟) 如图，在矩形ABCD中，点O为对角线AC、BD的交点，点E为BC上一点，连接EO，并延长交AD于点F，则图中全等三角形共有（）

A . 5对 B . 6对 C . 8对 D . 10对

答案解析收藏纠错 + 选题
5. (2018·固镇模拟) 如图，在一个长方体上放着一个小正方体，若这个组合体的俯视图如图所示，则这个组合体的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2017·杭州模拟) 若a是不等式2x﹣1＞5的解，b不是不等式2x﹣1＞5的解，则下列结论正确的是（）

A . a＞b B . a≥b C . a＜b D . a≤b

答案解析收藏纠错 + 选题
7. (2020九上·厦门期中) 两年前生产1吨甲种药品的成本是5000元．随着生产技术的进步，成本逐年下降，第2年的年下降率是第1年的年下降率的2倍，现在生产1吨甲种药品成本是2400元．为求第一年的年下降率，假设第一年的年下降率为x，则可列方程（）

A . 5000（1﹣x﹣2x）=2400 B . 5000（1﹣x）²=2400 C . 5000﹣x﹣2x=2400 D . 5000（1﹣x）（1﹣2x）=2400

答案解析收藏纠错 + 选题
8. (2021九上·吉林期末)
如图，在平面直角坐标系xOy中，抛物线y=x²+bx+c与x轴只有一个交点M，与平行于x轴的直线l交于A、B两点，若AB=3，则点M到直线l的距离为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023九下·淳安期中) 如图，AB是⊙的直径，CD是∠ACB的平分线交⊙O于点D，过D作⊙O的切线交CB的延长线于点E．若AB=4，∠E=75°，则CD的长为（）

A . $\text{[math]}$ B . 2 C . 2 $\text{[math]}$ D . 3 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2017·河南模拟)
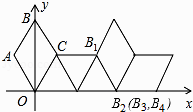
如图，在坐标系中放置一菱形OABC，已知∠ABC=60°，点B在y轴上，OA=1，先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2017次，点B的落点依次为B₁ ， B₂ ， B₃ ， …，则B₂₀₁₇的坐标为（）

A . （1345，0） B . （1345.5， $\text{[math]}$ ） C . （1345， $\text{[math]}$ ） D . （1345.5，0）

答案解析收藏纠错 + 选题

二、填空题

11. (2019·广东模拟) 分解因式：ma²﹣4ma+4m=．

答案解析收藏纠错 + 选题
12. 若关于x的一元二次方程x²﹣2x﹣k=0没有实数根，则k的取值范围是

答案解析收藏纠错 + 选题
13. (2017·杭州模拟) 如图，AB是⊙O的直径，AB=15，AC=9，则tan∠ADC=．

答案解析收藏纠错 + 选题
14. (2017·杭州模拟) 如图所示，在△ABC中，AB=6，AC=4，P是AC的中点，过P点的直线交AB于点Q，若以A、P、Q为顶点的三角形和以A、B、C为顶点的三角形相似，则AQ的长为．

答案解析收藏纠错 + 选题
15. (2017·杭州模拟) 如图，△ABC中，AD⊥BC，垂足为D，AD=BD=3，CD=2，点E从点B出发沿线段BA的方向移动到点A停止，连接CE．若△ADE与△CDE的面积相等，则线段DE的长度是．

答案解析收藏纠错 + 选题
16. (2017·微山模拟) 如图，在△ABC中，∠C=90°，AC=BC，斜边AB=2，O是AB的中点，以O为圆心，线段OC的长为半径画圆心角为90°的扇形OEF，弧EF经过点C，则图中阴影部分的面积为．

答案解析收藏纠错 + 选题

三、解答题

17. (2017·杭州模拟) 计算：（ $\text{[math]}$ ）^﹣2+（π﹣2017）⁰+sin60°+| $\text{[math]}$ ﹣2|

答案解析收藏纠错 + 选题
18. (2017·杭州模拟) 某学校要举办一次演讲比赛，每班只能选一人参加比赛．但八年级一班共有甲、乙两人的演讲水平相不相上下，现要在他们两人中选一人去参加全校的演讲比赛，经班主任与全班同学协商决定用摸小球的游戏来确定谁去参赛（胜者参赛）．
游戏规则如下：在两个不透明的盒子中，一个盒子里放着两个红球，一个白球；另一个盒子里放着三个白球，一个红球，从两个盒子中各摸一个球，若摸得的两个球都是红球，甲胜；摸得的两个球都是白球，乙胜，否则，视为平局．若为平局，继续上述游戏，直至分出胜负为止．
根据上述规则回答下列问题：
1. （1）从两个盒子各摸出一个球，一个球为白球，一个球为红球的概率是多少？
2. （2）该游戏公平吗？请用列表或树状图等方法说明理由．
答案解析收藏纠错 + 选题
19. (2017·杭州模拟) 随着人们经济收入的不断提高，汽车已越来越多地进入到各个家庭．某大型超市为缓解停车难问题，建筑设计师提供了楼顶停车场的设计示意图．按规定，停车场坡道口上坡要张贴限高标志，以便告知车辆能否安全驶入．如图，地面所在的直线ME与楼顶所在的直线AC是平行的，CD的厚度为0.5m，求出汽车通过坡道口的限高DF的长（结果精确到0.1m，sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）．

答案解析收藏纠错 + 选题
20. (2017·杭州模拟) 如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，﹣2）．
1. （1）求直线AB的解析式；
2. （2）若直线AB上的点C在第一象限，且S_△BOC=2，求经过点C的反比例函数的解析式．
答案解析收藏纠错 + 选题
21. (2017·杭州模拟) 如图，AB是⊙O的直径，点C在⊙O上，∠ABC的平分线与AC相交于点D，与⊙O过点A的切线相交于点E．
1. （1） ∠ACB=°，理由是：；
2. （2）猜想△EAD的形状，并证明你的猜想；
3. （3）若AB=8，AD=6，求BD．
答案解析收藏纠错 + 选题
22. (2017·杭州模拟)
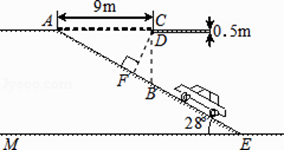
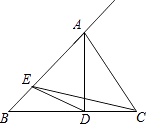
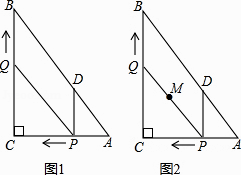
如图1，在Rt△ABC中，∠C=90°，AC=6，BC=8，动点P从点A开始沿边AC向点C以1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD//BC，交AB于点D，连接PQ分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒（t≥0）．
1. （1）直接用含t的代数式分别表示：QB=，PD=．
2. （2）是否存在t的值，使四边形PDBQ为菱形？若存在，求出t的值；若不存在，说明理由．并探究如何改变Q的速度（匀速运动），使四边形PDBQ在某一时刻为菱形，求点Q的速度；
3. （3）如图2，在整个运动过程中，求出线段PQ中点M所经过的路径长．
答案解析收藏纠错 + 选题
23. (2017·杭州模拟)
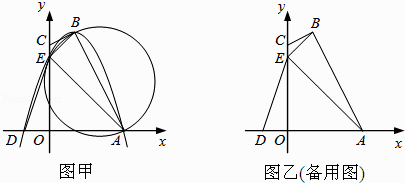
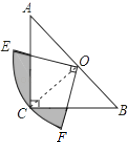
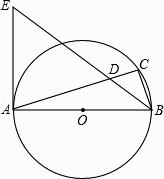
如图甲，四边形OABC的边OA、OC分别在x轴、y轴的正半轴上，顶点在B点的抛物线交x轴于点A、D，交y轴于点E，连接AB、AE、BE．已知tan∠CBE= $\text{[math]}$ ，A（3，0），D（﹣1，0），E（0，3）．
1. （1）求抛物线的解析式及顶点B的坐标；
2. （2）求证：CB是△ABE外接圆的切线；
3. （3）试探究坐标轴上是否存在一点P，使以D、E、P为顶点的三角形与△ABE相似，若存在，直接写出点P的坐标；若不存在，请说明理由；
4. （4）设△AOE沿x轴正方向平移t个单位长度（0＜t≤3）时，△AOE与△ABE重叠部分的面积为s，求s与t之间的函数关系式，并指出t的取值范围．
答案解析收藏纠错 + 选题