浙江省嘉兴市秀洲区、经开区七校联考2019-2020学年八年...

更新时间：2024-07-13 浏览次数：307 类型：期中考试

一、选择题（本题有10小题，每小题3分，共30分）

1. (2019八上·秀洲期中) 下列各组长度的线段能构成三角形的是 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019八上·秀洲期中) 在 $\text{[math]}$ 中，已知 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022八上·北仑期中) 下列命题是真命题的是 $\text{[math]}$ $\text{[math]}$

A . 相等的角是对顶角 B . 若实数 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ C . 若实数 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ D . 两直线平行，内错角相等

答案解析收藏纠错 + 选题
4. (2021八上·南丹期末) 下列四个图案中，不是轴对称图案的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2022八上·宁波期末) 要说明命题“若 $\text{[math]}$ ，则 $\text{[math]}$ ”是假命题，能举的一个反例是 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024七下·龙马潭月考) 若 $\text{[math]}$ 成立，则下列不等式成立的是 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022八上·重庆市开学考) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的中线， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的周长和 $\text{[math]}$ 的周长差为 $\text{[math]}$ $\text{[math]}$

A . 6 B . 3 C . 2 D . 不确定

答案解析收藏纠错 + 选题
8. (2020八上·赣榆期中) 已知一个等腰三角形一内角的度数为 $\text{[math]}$ ，则这个等腰三角形顶角的度数为 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2019八上·秀洲期中) 如图A所示，将长为20cm，宽为2cm的长方形白纸条，折成图B所示的图形并在其一面着色，则着色部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2019八上·秀洲期中) 如图，已知 $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ ，则下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；其中正确结论的个数是 $\text{[math]}$ $\text{[math]}$

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（本题有10小题，每小题3分，共30分）

11. (2019八上·秀洲期中) 命题“如果 $\text{[math]}$ ，那么 $\text{[math]}$ ”是命题（填“真”或“假” $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2019八上·秀洲期中) 如图，数轴上所表示的关于 $\text{[math]}$ 的不等式是．

答案解析收藏纠错 + 选题
13. (2019八上·秀洲期中) 如图， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
14. (2019八上·秀洲期中) 如图，已知 $\text{[math]}$ 判定 $\text{[math]}$ 时，还需添加的条件是．

答案解析收藏纠错 + 选题
15. (2019八上·秀洲期中) 等边三角形的边长为 $\text{[math]}$ ，则它的周长为，等边三角形共有条对称轴．

答案解析收藏纠错 + 选题
16. (2019八上·秀洲期中) 如图，直线 $\text{[math]}$ ， $\text{[math]}$ 的顶点 $\text{[math]}$ 在直线 $\text{[math]}$ 上， $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
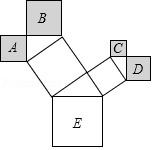
17. (2019八上·秀洲期中) 一株美丽的勾股树如图所示，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的面积分别为2，5，1，2，则最大的正方形 $\text{[math]}$ 的面积是．

答案解析收藏纠错 + 选题
18. (2019八上·秀洲期中) 如图，正方形 $\text{[math]}$ 中， $\text{[math]}$ ，以0为圆心， $\text{[math]}$ 为半径画弧交数轴于点 $\text{[math]}$ ．则点 $\text{[math]}$ 表示的数是．

答案解析收藏纠错 + 选题
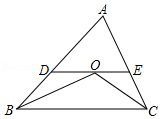
19. (2019八上·秀洲期中) 如图， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 和 $\text{[math]}$ 的平分线， $\text{[math]}$ 与 $\text{[math]}$ 相交于 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的平行线交 $\text{[math]}$ 于 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的周长是．

答案解析收藏纠错 + 选题
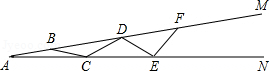
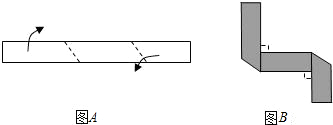
20. (2020八上·武安期末) 如图， $\text{[math]}$ 是一个钢架结构，已知 $\text{[math]}$ ，在角内部构造钢条 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 且满足 $\text{[math]}$ 则这样的钢条最多可以构造根．

答案解析收藏纠错 + 选题

三、解答题（本大题6小题，第21-24题每题6分，第25题、26题每题8分，共40分）

21. (2019八上·秀洲期中) 解下列不等式（组 $\text{[math]}$ ．
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
22. (2019八上·秀洲期中) 已知：如图，点 $\text{[math]}$ 在 $\text{[math]}$ 上，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ 和 $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
23. (2019八上·秀洲期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上一点（点 $\text{[math]}$ 与点 $\text{[math]}$ ，点 $\text{[math]}$ 不重合），连结 $\text{[math]}$ 在 $\text{[math]}$ 的右侧作等腰直角三角形 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
24. (2019八上·秀洲期中) 某校为提升硬件设施，决定采购80台电脑，现有 $\text{[math]}$ ， $\text{[math]}$ 两种型号的电脑可供选择．已知每台 $\text{[math]}$ 型电脑比 $\text{[math]}$ 型的贵2000元，2台 $\text{[math]}$ 型电脑与3台 $\text{[math]}$ 型电脑共需24000元．
1. （1）分别求 $\text{[math]}$ ， $\text{[math]}$ 两种型号电脑的单价；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ 两种型号电脑的采购总价不高于38万元，则 $\text{[math]}$ 型电脑最多采购多少台？
答案解析收藏纠错 + 选题
25. (2019八上·秀洲期中) 如图，折叠长方形纸片 $\text{[math]}$ 的一边 $\text{[math]}$ ，使点 $\text{[math]}$ 落在 $\text{[math]}$ 边的点 $\text{[math]}$ 处，已知 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求线段 $\text{[math]}$ 的长；
2. （2）求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
26. (2019八上·秀洲期中) 问题背景：
1. （1）如图1：在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ． $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 上的点．且 $\text{[math]}$ ．探究图中线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系．小王同学探究此问题的方法是，延长 $\text{[math]}$ 到点 $\text{[math]}$ ．使 $\text{[math]}$ ．连结 $\text{[math]}$ ，先证明 $\text{[math]}$ ，再证明 $\text{[math]}$ ，可得出结论，他的结论应是．
  探索延伸：
2. （2）如图2，若在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ． $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 上的点，且 $\text{[math]}$ ，上述结论是否仍然成立，并说明理由．
答案解析收藏纠错 + 选题