 B .
B .  C .
C .  D .
D . 
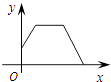 B .
B . 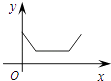 C .
C .  D .
D . 
队员甲 | 队员乙 | 队员丙 | 队员丁 | |
平均数 | 45 | 46 | 45 | 46 |
方差 | 1.5 | 1.5 | 3.5 | 4.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
如图所示,在矩形纸片 中,
,
为
边上两点,且
;
,
为
边上两点,且
.沿虚线
折叠,使点
落在点
上,点
落在点
上;然后再沿虚线
折叠,使
落在点
上,点
落在点
上.叠完后,剪一个直径在
上的半圆,再展开,则展开后的图形为( )

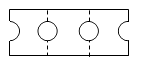 B .
B .  C .
C .  D .
D . 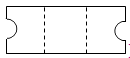
身高/cm | 146 | 151 | 153 | 154 | 156 | 157 | 158 | 159 | 160 |
人数 | 1 | 2 | 2 | 2 | 3 | 4 | 8 | 4 | 4 |
身高/cm | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 169 | |
人数 | 2 | 4 | 3 | 2 | 3 | 4 | 1 | 1 |
根据下表的分组方法进行数据整理,补全频数分布表:

① 根据题意完成作图;
② 猜想线段 ,
的数量关系,并写出你的证明思路.
我们对平面直角坐标系 中的三角形给出新的定义:三角形的“横长”和三角形的“纵长”.我们假设点
,
是三角形边上的任意两点.如果
的最大值为
,那么三角形的“横长”
;如果
的最大值为
,那么三角形的“纵长”
.如右图,该三角形的“横长”
;“纵长”
.
当 时,我们管这样的三角形叫做“方三角形”.

如图1所示,

已知点 ,
.
在点 ,
,
中,可以和点
,点
构成“方三角形”的点是;
如图2所示,已知点 ,
,点
为平面直角坐标系中任意一点.若
为“方三角形”,且
,请直接写出点
的坐标.
